题目内容
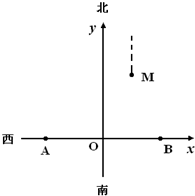
如图,相距200海里的A、B两地分别有救援A船和B船.在接到求救信息后,A船能立即出发,B船因港口原因需2小时后才能出发,两船的航速都是30海里/小时.在同时收到求救信息后,A船早于B船到达的区域称为A区,否则称为B区.若在A地北偏东45°方向,距A地150
海里处的M点有一艘遇险船正以10海里/小时的速度向正北方向漂移.A区与B区边界线(即A、B两船能同时到达的点的轨迹)方程;
问:
①应派哪艘船前往救援?
②救援船最快需多长时间才能与遇险船相遇?(精确到0.1小时)
| 2 |
问:
①应派哪艘船前往救援?
②救援船最快需多长时间才能与遇险船相遇?(精确到0.1小时)

设点P为边界线上的点,由题意知
=
+2,即PA-PB=60,
∴动点P到两定点A、B的距离之差为常数,
∴点P的轨迹是双曲线中的一支.…(3分)
由2c=200,2a=60得a=30,b2=1002-302=9100
∴方程为
-
=1(x>0)…(6分)
①M点的坐标为M(50,150),A点的坐标为A(-100,0),B点的坐标为B(100,0),
∴|MA|=150
≈212.1,|MB|=
≈158.1,
∴|MA|-|MB|≈212.1-158.1=54<60,
∴点M在A区,又遇险船向正北方向漂移,即遇险船始终在A区内,
∴应派A船前往救援…(8分)
②设经t小时后,A救援船在点N处与遇险船相遇.
在△AMN中,AM=150
,MN=10t,AN=30t,∠AMN=135°…(9分)
∴(30t)2=(10t)2+(150
)2-2•10t•150
cos135°
整理得4t2-15t-225=0,
解得t=
≈9.606或t=
(舍)…(13分)
∴A救援船需9.6小时后才能与遇险船相遇.…(14分)
| PA |
| 30 |
| PB |
| 30 |
∴动点P到两定点A、B的距离之差为常数,
∴点P的轨迹是双曲线中的一支.…(3分)
由2c=200,2a=60得a=30,b2=1002-302=9100
∴方程为
| x2 |
| 900 |
| y2 |
| 9100 |
①M点的坐标为M(50,150),A点的坐标为A(-100,0),B点的坐标为B(100,0),
∴|MA|=150
| 2 |
| 502+1502 |
∴|MA|-|MB|≈212.1-158.1=54<60,
∴点M在A区,又遇险船向正北方向漂移,即遇险船始终在A区内,
∴应派A船前往救援…(8分)
②设经t小时后,A救援船在点N处与遇险船相遇.
在△AMN中,AM=150
| 2 |
∴(30t)2=(10t)2+(150
| 2 |
| 2 |
整理得4t2-15t-225=0,
解得t=
15+15
| ||
| 8 |
15-15
| ||
| 8 |
∴A救援船需9.6小时后才能与遇险船相遇.…(14分)

练习册系列答案
相关题目
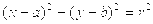 的圆心为抛物线
的圆心为抛物线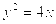 的焦点,直线3x+4y+2=0与圆C相切,则该圆的方程为( ).
的焦点,直线3x+4y+2=0与圆C相切,则该圆的方程为( ).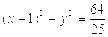
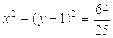
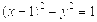
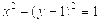
 的直线与抛物线在x轴上方部分相交于点A,则AF= .
的直线与抛物线在x轴上方部分相交于点A,则AF= .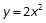 的焦点坐标是( ) .
的焦点坐标是( ) .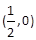
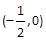
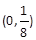
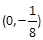
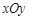 中,抛物线
中,抛物线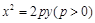 上纵坐标为2的一点到焦点的距离为3,则抛物线的焦点坐标为 .
上纵坐标为2的一点到焦点的距离为3,则抛物线的焦点坐标为 .