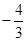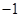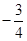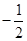题目内容
若双曲线
-
=1(a>0,b>0)的渐近线与抛物线x2=4y的准线所围成的三角形面积为2,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A.
| B.
| C.
| D.
|
抛物线x2=4y的准线方程为y=-1,双曲线
-
=1的两条渐近线方程为y=±
x,
∴抛物线的准线与双曲线的两条渐近线的交点坐标为(±
,-1),
∴抛物线的准线与双曲线的两条渐近线所围成的三角形的面积是
•
•2=2,
∴
=2,
∴b=
a,
∴c=
=
a,
∴e=
=
.
故选:A.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
∴抛物线的准线与双曲线的两条渐近线的交点坐标为(±
| a |
| b |
∴抛物线的准线与双曲线的两条渐近线所围成的三角形的面积是
| 1 |
| 2 |
| a |
| b |
∴
| a |
| b |
∴b=
| 1 |
| 2 |
∴c=
| a2+b2 |
| ||
| 2 |
∴e=
| c |
| a |
| ||
| 2 |
故选:A.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
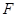 上,且灯的深度
上,且灯的深度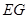 等于灯口直径
等于灯口直径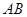 ,且为64
,且为64 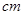 ,则光源安装的位置
,则光源安装的位置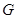 的距离为____________
的距离为____________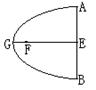
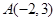 在抛物线C:
在抛物线C: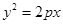 的准线上,记C的焦点为F,则直线AF的斜率为( )
的准线上,记C的焦点为F,则直线AF的斜率为( )