题目内容
设F1是椭圆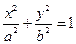 (a>b>0)的一个焦点,PQ是经过另一个焦点F2的弦,则△PF1Q的周长是( )
(a>b>0)的一个焦点,PQ是经过另一个焦点F2的弦,则△PF1Q的周长是( )
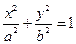 (a>b>0)的一个焦点,PQ是经过另一个焦点F2的弦,则△PF1Q的周长是( )
(a>b>0)的一个焦点,PQ是经过另一个焦点F2的弦,则△PF1Q的周长是( )| A.4a | B.4b | C.2a | D.2b |
A
依题意,椭圆的周长L=|PQ|+|PF1|+|QF1|=|PF2|+|PF1|+|QF1|+|QF2|=2a+2a=4a,选择A

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 为坐标原点,
为坐标原点, 为椭圆
为椭圆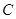 :
: 在
在 轴正半轴上的焦点,过
轴正半轴上的焦点,过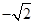 的直线
的直线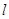 与
与 、
、 两点,点
两点,点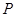 满足
满足 .
.
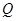 ,证明:
,证明: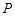 在椭圆
在椭圆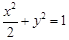 上,
上,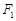 、
、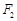 分别是该椭圆的两焦点,且
分别是该椭圆的两焦点,且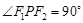 ,则
,则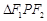 的面积是( )
的面积是( )
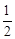
 的焦点为顶点,顶点为焦点的椭圆方程为
的焦点为顶点,顶点为焦点的椭圆方程为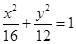

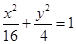

 题满分13分)
题满分13分)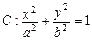 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆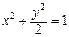 有相同的离心率,斜
有相同的离心率,斜 ),与椭圆C交于不同两点A、B.
),与椭圆C交于不同两点A、B. ,两个焦点为
,两个焦点为 ,
,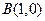 ,O为坐标原点。
,O为坐标原点。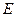 经过点
经过点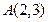 ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点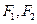 在
在 轴上,离心率
轴上,离心率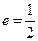 ,
,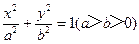 的左、右焦点分别是F1,F2,过F2作倾斜角为
的左、右焦点分别是F1,F2,过F2作倾斜角为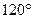 的直线与椭圆的一个交点为M,若MF1垂直于x轴,则椭圆的离心率为______
的直线与椭圆的一个交点为M,若MF1垂直于x轴,则椭圆的离心率为______ 的两焦点为F1,F2,一直线过F1交椭圆于P、Q,则△PQF2的周长为 ___________.
的两焦点为F1,F2,一直线过F1交椭圆于P、Q,则△PQF2的周长为 ___________.