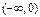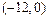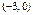题目内容
(本小 题满分13分)
题满分13分)
已知椭圆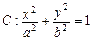 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆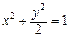 有相同的离心率,斜
有相同的离心率,斜
率为k的直线l经过点M(0,1 ),与椭圆C交于不同两点A、B.
),与椭圆C交于不同两点A、B.
(1)求椭圆C的标准方程;
(2)当椭圆C的右焦点F在以AB为直径的圆内时,求k的取值范围.
 题满分13分)
题满分13分)已知椭圆
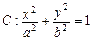 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆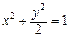 有相同的离心率,斜
有相同的离心率,斜率为k的直线l经过点M(0,1
 ),与椭圆C交于不同两点A、B.
),与椭圆C交于不同两点A、B.(1)求椭圆C的标准方程;
(2)当椭圆C的右焦点F在以AB为直径的圆内时,求k的取值范围.
解:(1)∵焦距为4,∴ c=2………………………………………………1分
c=2………………………………………………1分
又∵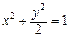 的离心率为
的离心率为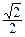 ……………………………… 2分
……………………………… 2分
∴ ,∴a=
,∴a=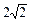 ,b=2………………………… 4分
,b=2………………………… 4分
∴标准方程为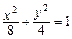 ………………………………………6分
………………………………………6分
(2)设直线l方程:y=kx+1,A(x1,y1),B(x2,y2),
由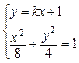 得
得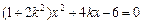 ……………………7分
……………………7分
∴x1+x2=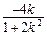 ,x1x2=
,x1x2=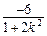
由(1)知右焦点F坐标为(2,0),
∵右焦点F在圆内部,∴ <0………………………………8分
<0………………………………8分
∴(x1 -2)(x2-2)+ y1y2<0
即x1x2-2(x1+x2)+4+k2 x1x2+k(x1+x2)+1<0…………………… 9分
∴ <0…………… 11分
<0…………… 11分
∴k<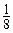 ……………………………………………………………… 12分
……………………………………………………………… 12分
经检验得k<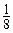 时,直线l与椭圆相交,
时,直线l与椭圆相交,
∴直线l的斜率k的范围为(-∞,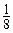 )……………………………13
)……………………………13
 c=2………………………………………………1分
c=2………………………………………………1分又∵
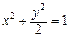 的离心率为
的离心率为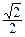 ……………………………… 2分
……………………………… 2分∴
 ,∴a=
,∴a=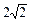 ,b=2………………………… 4分
,b=2………………………… 4分∴标准方程为
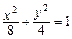 ………………………………………6分
………………………………………6分(2)设直线l方程:y=kx+1,A(x1,y1),B(x2,y2),
由
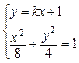 得
得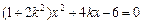 ……………………7分
……………………7分∴x1+x2=
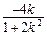 ,x1x2=
,x1x2=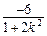
由(1)知右焦点F坐标为(2,0),
∵右焦点F在圆内部,∴
 <0………………………………8分
<0………………………………8分∴(x1 -2)(x2-2)+ y1y2<0
即x1x2-2(x1+x2)+4+k2 x1x2+k(x1+x2)+1<0…………………… 9分
∴
 <0…………… 11分
<0…………… 11分∴k<
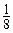 ……………………………………………………………… 12分
……………………………………………………………… 12分经检验得k<
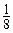 时,直线l与椭圆相交,
时,直线l与椭圆相交,∴直线l的斜率k的范围为(-∞,
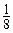 )……………………………13
)……………………………13略

练习册系列答案
相关题目
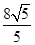 B
B 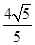 C
C 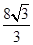 D
D 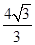
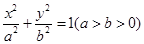 的左准线上,过点P斜率为
的左准线上,过点P斜率为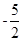 的光线,
的光线,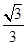
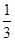
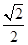
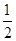
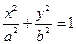 (a>b>0)的一个焦点,PQ是经过另一个焦点F2的弦,则△PF1Q的周长是( )
(a>b>0)的一个焦点,PQ是经过另一个焦点F2的弦,则△PF1Q的周长是( )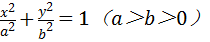 上的动点Q,过动点Q作椭圆的切线l,过右焦点作l的垂线,垂足为P,则点P的轨迹方程为( )
上的动点Q,过动点Q作椭圆的切线l,过右焦点作l的垂线,垂足为P,则点P的轨迹方程为( )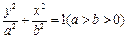 的右顶点与上顶点分别
的右顶点与上顶点分别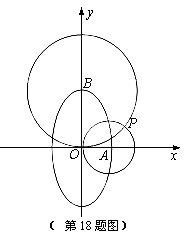
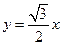 上,求椭圆的离心率;
上,求椭圆的离心率;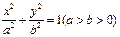 中心的直线与椭圆交于A、B两点,右焦点为F2,则△ABF2
中心的直线与椭圆交于A、B两点,右焦点为F2,则△ABF2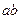 B.
B.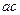 C.
C.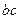 D.
D.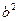





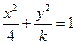 的离心率
的离心率 ,则
,则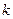 的取值范围是 ( )
的取值范围是 ( )