题目内容
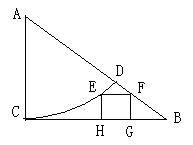
(本小题满分12分)在△ABC中,∠C = 90o ,BC = 1.以A为圆心,AC为半径画弧交AB于D,在由弧CD与直线段BD、BC所围成的范围内作内接正方形EFGH(如图)。设AC = x,EF =" y" ,(1)求y与x的函数关系式;(2)正方形EFGH的面积是否有最大值?试证明你的结论。

(1)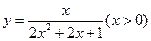 (2)略
(2)略
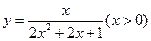 (2)略
(2)略(本题满分12分)

(1)延长FE与AB交于点P,则∵EP//BC,∴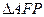 ∽
∽ ,
,
∴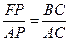 ,即
,即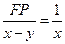 ,∴
,∴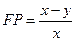 , …………2分
, …………2分
在直角三角形AEP中,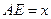 ,
,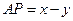 ,
,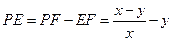 ,
,
由勾股定理,得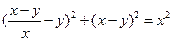 (*)即
(*)即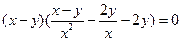 。……6分
。……6分
∵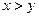 ∴(*)式成立的充要条件是
∴(*)式成立的充要条件是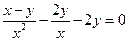 ,
,
所以y与x的函数关系式为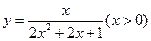 , ……8分
, ……8分
(2)因为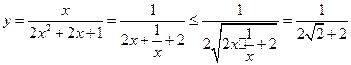 ,等号当且仅当
,等号当且仅当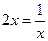 ,即
,即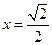 时取得10分 所以正方形
时取得10分 所以正方形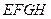 的面积
的面积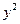 当
当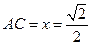 时取得最大值
时取得最大值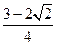 12分
12分
若由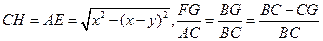 得
得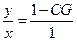 ,
,
所以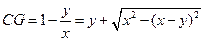 即
即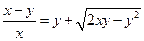 ,
,
等式右端分子有理化,得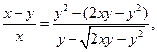
∴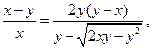 ∵
∵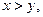 ∴
∴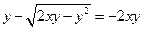 ,
,
整理,得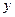 与
与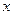 的函数关系式为
的函数关系式为 (
(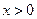 )
)

(1)延长FE与AB交于点P,则∵EP//BC,∴
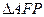 ∽
∽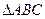 ,
,∴
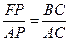 ,即
,即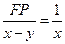 ,∴
,∴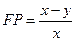 , …………2分
, …………2分在直角三角形AEP中,
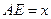 ,
,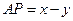 ,
,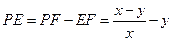 ,
,由勾股定理,得
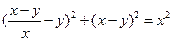 (*)即
(*)即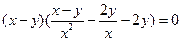 。……6分
。……6分∵
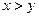 ∴(*)式成立的充要条件是
∴(*)式成立的充要条件是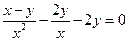 ,
,所以y与x的函数关系式为
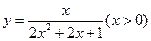 , ……8分
, ……8分(2)因为
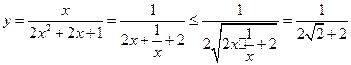 ,等号当且仅当
,等号当且仅当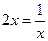 ,即
,即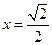 时取得10分 所以正方形
时取得10分 所以正方形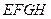 的面积
的面积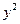 当
当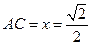 时取得最大值
时取得最大值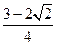 12分
12分若由
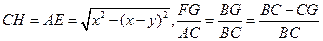 得
得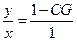 ,
,所以
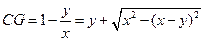 即
即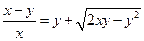 ,
,等式右端分子有理化,得
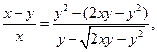
∴
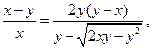 ∵
∵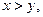 ∴
∴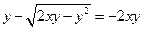 ,
,整理,得
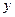 与
与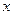 的函数关系式为
的函数关系式为 (
(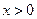 )
)
练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
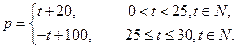 该商品的日销售量Q(件)与时间t(天)的函数关系是
该商品的日销售量Q(件)与时间t(天)的函数关系是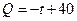
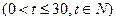 ,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?
,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?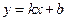 与二次函数
与二次函数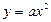 图像如图,其中
图像如图,其中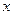 轴、
轴、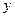 轴的交点分别为A(2,0),B(0,2);与二次函数
轴的交点分别为A(2,0),B(0,2);与二次函数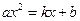
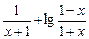 .
.  )]<
)]< ,g(x)=
,g(x)= 的图象的示意图如图所示,
的图象的示意图如图所示, )B(
)B(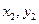 ),且
),且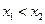
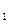 ,C
,C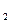 分别对应哪一个函数?
分别对应哪一个函数? 且
且 ,指出a,b的值,并说明理由;
,指出a,b的值,并说明理由; 1
1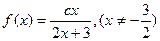 满足
满足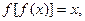 则常数
则常数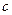 等于( )
等于( )