题目内容
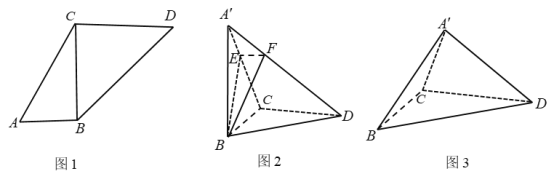
【题目】在四棱锥![]() 中,底面
中,底面![]() 是菱形,且
是菱形,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
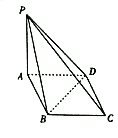
(1)证明:![]() 平面
平面![]() .
.
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析(2)![]()
【解析】
(1)先连接![]() ,AC与BD交点为E,连接PE,先证直线
,AC与BD交点为E,连接PE,先证直线![]() 平面
平面![]() ,进而可得
,进而可得![]() ,再由
,再由![]() ,
,![]() ,即可得出
,即可得出![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,由题意可得EB、EC、EF两两垂直,因此以E点为坐标原点建立坐标系,分别求出两平面的一个法向量,进而求两法向量夹角余弦值,由题中图形判断二面角时锐角还是钝角,即可求出二面角的余弦值.
,由题意可得EB、EC、EF两两垂直,因此以E点为坐标原点建立坐标系,分别求出两平面的一个法向量,进而求两法向量夹角余弦值,由题中图形判断二面角时锐角还是钝角,即可求出二面角的余弦值.
(1)证明:连接![]() ,设
,设![]() ,连接
,连接![]() .
.
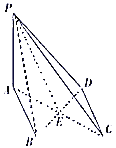
因为底面![]() 是菱形,所以
是菱形,所以![]() ,
,![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
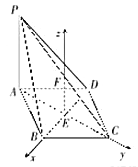
(2)解:取![]() 的中点
的中点![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
故以![]() 为原点,
为原点,![]() 分别为
分别为![]() 的正方向建立如图所示的空间直角坐标系
的正方向建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
故![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() .
.
则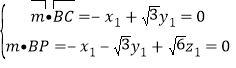 ,不妨取
,不妨取![]() ,则
,则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则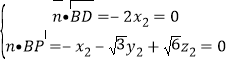 ,不妨取
,不妨取![]() ,则
,则![]() .
.
记二面角![]() 的平面角为
的平面角为![]() ,易知
,易知![]() 为锐角,
为锐角,
则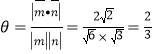 .
.
故二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】新冠肺炎疫情期间,为确保“停课不停学”,各校精心组织了线上教学活动.开学后,某校采用分层抽样的方法从三个年级的学生中抽取一个容量为150的样本进行关于线上教学实施情况的问卷调查.已知该校高一年级共有学生660人,抽取的样本中高二年级有50人,高三年级有45人.下表是根据抽样调查情况得到的高二学生日睡眠时间(单位:h)的频率分布表.
分组 | 频数 | 频率 |
| 5 | 0.10 |
| 8 | 0.16 |
| x | 0.14 |
| 12 | y |
| 10 | 0.20 |
| z | |
合计 | 50 | 1 |
(1)求该校学生总数;
(2)求频率分布表中实数x,y,z的值;
(3)已知日睡眠时间在区间[6,6.5)的5名高二学生中,有2名女生,3名男生,若从中任选2人进行面谈,则选中的2人恰好为一男一女的概率.
【题目】某工厂共有男女员工500人,现从中抽取100位员工对他们每月完成合格产品的件数统计如下:
每月完成合格产品的件数(单位:百件) |
|
|
|
|
|
频数 | 10 | 45 | 35 | 6 | 4 |
男员工人数 | 7 | 23 | 18 | 1 | 1 |
(1)其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面![]() 列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
非“生产能手” | “生产能手” | 合计 | |
男员工 | |||
女员工 | |||
合计 |
(2)为提高员工劳动的积极性,工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的,计件单价为1元;超出![]() 件的部分,累进计件单价为1.2元;超出
件的部分,累进计件单价为1.2元;超出![]() 件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
附:![]() ,
,
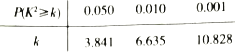 .
.
【题目】北京地铁八通线西起四惠站,东至土桥站,全长18.964km,共设13座车站.目前八通线执行2014年12月28日制订的计价标准,各站间计程票价(单位:元)如下:
四惠 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
四惠东 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
高碑店 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | p>5 | |||
传媒大学 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
双桥 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
管庄 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
八里桥 | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
通州北苑 | 3 | 3 | 3 | 3 | 3 | ||||||||
果园 | 3 | 3 | 3 | 3 | |||||||||
九棵树 | 3 | 3 | 3 | ||||||||||
梨园 | /p> | 3 | 3 | ||||||||||
临河里 | 3 | ||||||||||||
土桥 | |||||||||||||
四惠 | 四惠东 | 高碑店 | 传媒大学 | 双桥 | 管庄 | 八里桥 | 通州北苑 | 果园 | 九棵树 | 梨园 | 临河里 | 土桥 |
(Ⅰ)在13座车站中任选两个不同的车站,求两站间票价不足5元的概率;
(Ⅱ)甲乙二人从四惠站上车乘坐八通线,各自任选另一站下车(二人可同站下车),记甲乙二人乘车购票花费之和为X元,求X的分布列;
(Ⅲ)若甲乙二人只乘坐八通线,甲从四惠站上车,任选另一站下车,记票价为![]() 元;乙从土桥站上车,任选另一站下车,记票价为
元;乙从土桥站上车,任选另一站下车,记票价为![]() 元.试比较
元.试比较![]() 和
和![]() 的方差
的方差![]() 和
和![]() 大小.(结论不需要证明)
大小.(结论不需要证明)