题目内容
【题目】已知函数![]()
![]() .
.
(1)若![]() 在
在![]() 处有极值,问是否存在实数m,使得不等式
处有极值,问是否存在实数m,使得不等式![]() 对任意
对任意![]() 及
及![]() 恒成立?若存在,求出m的取值范围;若不存在,请说明理由.
恒成立?若存在,求出m的取值范围;若不存在,请说明理由.![]() ;
;
(2)若![]() ,设
,设![]() .
.
①求证:当![]() 时,
时,![]() ;
;
②设![]() ,求证:
,求证:![]()
【答案】(1)存在,![]() ;(2)①证明见解析;②证明见解析.
;(2)①证明见解析;②证明见解析.
【解析】
(1)根据微积分基本定理求得![]() ,由
,由![]() ,求得参数
,求得参数![]() ;利用导数求函数的在区间上的最值,结合一次不等式在区间上恒成立问题,即可求得参数
;利用导数求函数的在区间上的最值,结合一次不等式在区间上恒成立问题,即可求得参数![]() 的范围;
的范围;
(2)①求得![]() ,利用导数求得
,利用导数求得![]() 的单调性,即可容易证明;
的单调性,即可容易证明;
②由①中所求,可得![]() ,利用对数运算,即可证明.
,利用对数运算,即可证明.
由题可知![]() ,
,![]()
![]() .
.
(1)由![]() ,可得
,可得![]() ,
,![]() .
.
又当![]() 时,
时,![]() ,
,
故![]() 在区间
在区间![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
故函数![]() 在
在![]() 处取得极值,所以
处取得极值,所以![]() .
.
∵![]() ,
,![]() .
.
∴![]() ,
,
当![]() 时,由上述讨论可知,
时,由上述讨论可知,![]() 单调递增,
单调递增,
故![]()
不等式![]() 对任意
对任意![]() 及
及![]() 恒成立,
恒成立,
即:![]() ,
,
即:![]() 对
对![]() 恒成立,令
恒成立,令![]() ,
,
![]() ,
,![]()
即![]() ,且
,且![]() ,
,
整理得![]() ,且
,且![]() ,
,
解得:![]() ,即为所求.
,即为所求.
(2)①∵![]() ,
,![]()
![]()
当![]() 时,
时,![]() ,
,![]()
![]() 在
在![]() 上单调递减,
上单调递减,
![]() 即证.
即证.
②由①可得:![]()
令:![]() ,得
,得![]() ,即:
,即:![]()
![]()
![]() =
=![]()
即证.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案【题目】由国家公安部提出,国家质量监督检验检疫总局发布的《车辆驾驶人员血液、呼气酒精含量阀值与检验标准(GB/T19522-2010)》于2011年7月1日正式实施.车辆驾驶人员酒饮后或者醉酒后驾车血液中的酒精含量阀值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,且图表示的函数模型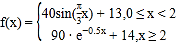 ,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:
,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:![]() ,
,![]() )
)
驾驶行为类型 | 阀值 |
饮酒后驾车 |
|
醉酒后驾车 |
|
车辆驾车人员血液酒精含量阀值

喝1瓶啤酒的情况
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】某企业共有员工10000人,下图是通过随机抽样得到的该企业部分员工年收入(单位:万元)频率分布直方图.
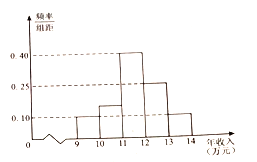
(1)根据频率分布直方图计算样本的平均数.并以此估算该企业全体员工中年收入不低于样本平均数的人数(同一组中的数据以这数据所在区间中点的值作代表);
(2)若抽样调查中收入在![]() 万元员工有2人,求在收入在
万元员工有2人,求在收入在![]() 万元的员工中任取3人,恰有2位员工收入在
万元的员工中任取3人,恰有2位员工收入在![]() 万元的概率;
万元的概率;
(3)若抽样调查的样本容量是400人,在这400人中:年收入在![]() 万元的员工中具有大学及大学以上学历的有
万元的员工中具有大学及大学以上学历的有![]() ,年收入在
,年收入在![]() 万元的员工中不具有大学及大学以上学历的有
万元的员工中不具有大学及大学以上学历的有![]() ,将具有大学及大学以上学历和不具有大学及大学以上学历的员工人数填入下面的列联表,并判断能否有
,将具有大学及大学以上学历和不具有大学及大学以上学历的员工人数填入下面的列联表,并判断能否有![]() 的把握认为具有大学及大学以上学历和不具有大学及大学以上学历的员工收入有差异?
的把握认为具有大学及大学以上学历和不具有大学及大学以上学历的员工收入有差异?
具有大学及大学以上学历 | 不具有大学及大学以上学历 | 合计 | |
| |||
| |||
合计 |
附:![]() ;
;
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |