题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,判断
时,判断![]() 零点个数并求出零点;
零点个数并求出零点;
(2)若函数![]() 存在两个不同的极值点
存在两个不同的极值点![]() ,
,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 只有一个零点,零点为0.(2)
只有一个零点,零点为0.(2)![]()
【解析】
(1)对函数![]() 求导,令
求导,令![]() ,对
,对![]() 求导,显然
求导,显然![]() ,
,![]() 可知
可知![]() 的单调性,特殊点
的单调性,特殊点![]() ,可知
,可知![]() 的单调性且
的单调性且![]() ,即可判定零点个数和零点;
,即可判定零点个数和零点;
(2)函数![]() 存在两个不同的极值点
存在两个不同的极值点![]() ,
,![]() ,等价于方程
,等价于方程![]() 有两个根,利用分类讨论思想,由(1)知,
有两个根,利用分类讨论思想,由(1)知,![]() 不合题意;当
不合题意;当![]() 时,讨论
时,讨论![]() 的单调性,其中分界点
的单调性,其中分界点![]() 和特殊点
和特殊点![]() ,通过构建函数
,通过构建函数![]() 比较
比较![]() 与
与![]() 大小可知
大小可知![]() ,由零点的存在性定理可知
,由零点的存在性定理可知![]() ,满足
,满足![]() ,得此类情况下由两个根;当
,得此类情况下由两个根;当![]() 时,
时,![]() ,无极值点;综上可得答案.
,无极值点;综上可得答案.
(1)由题知:![]() ,令
,令![]() ,
,![]() ,
,
当![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
因为![]() ,所以
,所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减,
单调递减,
所以![]() ,故
,故![]() 只有一个零点,零点为0.
只有一个零点,零点为0.
(2)函数![]() 存在两个不同的极值点
存在两个不同的极值点![]() ,
,![]() ,等价于方程
,等价于方程![]() 有两个根
有两个根
由(1)知:![]() 不合题意,
不合题意,
当![]() 时,因为
时,因为![]() ,
,![]() ,
,![]() 单调递增且
单调递增且![]() ,
,![]() ,
,![]() 单调递减;
单调递减;
又因为![]() 且
且![]() ,所以
,所以![]() ;
;
又因为![]() ,因为函数
,因为函数![]() ,
,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递减
上单调递减
所以![]() ,及
,及![]() ,所以存在
,所以存在![]() ,满足
,满足![]() ,
,
所以![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;
此时![]() 存在两个极值点
存在两个极值点![]() ,0,符合题意.
,0,符合题意.
当![]() 时,因为
时,因为![]() ,
,![]() ;
;![]() ,
,![]() ;
;
所以![]() ;所以
;所以![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 无极值点,不合题意;
无极值点,不合题意;
综上可得:![]() .
.

【题目】某校从2011年到2018年参加“北约”,“华约”考试而获得加分的学生(每位学生只能参加“北约”,“华约”一种考试)人数可以通过以下表格反映出来.(为了方便计算,将2011年编号为1,2012年编号为2,依此类推……)
年份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
人数y | 2 | 3 | 4 | 4 | 7 | 7 | 6 | 6 |
(1)据悉,该校2018年获得加分的6位同学中,有1位获得加20分,2位获得加15分,3位获得加10分,从该6位同学中任取两位,记该两位同学获得的加分之和为X,求X的分布列及期望.
(2)根据最近五年的数据,利用最小二乘法求出y与x之间的线性回归方程,并用以预测该校2019年参加“北约”,“华约”考试而获得加分的学生人数.(结果要求四舍五入至个位)
参考公式: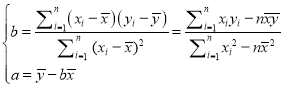
【题目】某产品的三个质量指标分别为x, y, z, 用综合指标S =" x" + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.