��Ŀ����
����Ŀ��ijУ��2011�굽2018��μӡ���Լ��������Լ�����Զ���üӷֵ�ѧ����ÿλѧ��ֻ�ܲμӡ���Լ��������Լ��һ�ֿ��ԣ���������ͨ�����±���ӳ��������Ϊ�˷�����㣬��2011����Ϊ1��2012����Ϊ2����������������
���x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
����y | 2 | 3 | 4 | 4 | 7 | 7 | 6 | 6 |
��1����Ϥ����У2018���üӷֵ�6λͬѧ�У���1λ��ü�20�֣�2λ��ü�15�֣�3λ��ü�10�֣��Ӹ�6λͬѧ����ȡ��λ���Ǹ���λͬѧ��õļӷ�֮��ΪX����X�ķֲ��м�������
��2�����������������ݣ�������С���˷����y��x֮������Իع鷽�̣�������Ԥ���У2019��μӡ���Լ��������Լ�����Զ���üӷֵ�ѧ�������������Ҫ��������������λ��
�ο���ʽ��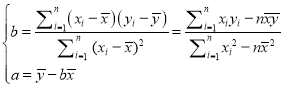
���𰸡���1����������![]() ����2��7��
����2��7��
��������
��1����λͬѧ��õļӷ�֮��ΪX���ӳ����ηֲ������ó����ηֲ��ĸ��ʹ�ʽ������ʣ��õ��ֲ��У����ý�.
��2���ɱ��е����ݣ���![]() ��
��![]() ��
��![]() ��
��![]() �����빫ʽ�����ý����Իع鷽��,�������ݽ���Ԥ�⼴��.
�����빫ʽ�����ý����Իع鷽��,�������ݽ���Ԥ�⼴��.
��1�������⣬����������п��ܵ�ֵΪ20��25��30��35
P��X��20��![]() ��P��X��25��
��P��X��25��![]() ��
��
P��X��30��![]() ��P��X��35��
��P��X��35��![]() ��
��
X | 20 | 25 | 30 | 35 |
P |
|
|
|
|
E��X��![]() ��
��
��2���ɱ��е����ݣ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
a![]() ��
��
�����Իع鷽��Ϊy��0.3x+4.2��
��x��9ʱ��y��0.3��9+4.2��6.9��
�ʸ�У2019��μ�����Լ��������Լ�����Զ���üӷֵ�ѧ������7��