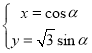题目内容
【题目】已知函数f(x)=ex﹣a(x2+x+1).
(1)当a=1时,证明:f(x)+x2≥0;
(2)当a![]() 时,判断函数f(x)的单调性;
时,判断函数f(x)的单调性;
(3)若函数f(x)有三个零点,求实数a的取值范围.
【答案】(1)见解析;(2)f(x)在R单调递增;(3)(![]() ,1)
,1)
【解析】
(1)令![]() ,通过求导证明
,通过求导证明![]() ,即可得证;
,即可得证;
(2)对![]() 求导,结合(1)中结论得
求导,结合(1)中结论得![]() ,即可得解;
,即可得解;
(3)由条件得![]() 有三个实根,令
有三个实根,令![]() ,求出导数后根据函数的单调性结合极值即可得解.
,求出导数后根据函数的单调性结合极值即可得解.
(1)当a=1时,f(x)+x2≥0等价于![]() ,
,
令![]() ,g′(x)=ex﹣1,
,g′(x)=ex﹣1,
可得g(x)在(﹣∞,0)递减,在(0,+∞)递增,∴![]() ,
,
∴ex﹣(x+1)≥0即f(x)+x2≥0;
(2)当![]() 时,
时,![]() .
.![]() ,
,
∴函数f(x)在R单调递增;
(3)函数f(x)有三个零点 ![]() 有三个实根,
有三个实根,
令![]() ,
,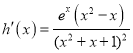 ,
,
∴h(x)在(﹣∞,0)递增,在(0,1)递减,在(1,+∞)递增,
且x→﹣∞时,h(x)→0,x→+∞时,h(x)→+∞,h(0)=1, ![]() ,
,
∴实数a的取值范围是(![]() ,1).
,1).

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案【题目】在新高考改革中,打破了文理分科的“![]() ”模式,不少省份采用了“
”模式,不少省份采用了“![]() ”,“
”,“![]() ”,“
”,“![]() ”等模式.其中“
”等模式.其中“![]() ”模式的操作又更受欢迎,即语数外三门为必考科目,然后在物理和历史中选考一门,最后从剩余的四门中选考两门.某校为了了解学生的选科情况,从高二年级的2000名学生(其中男生1100人,女生900人)中,采用分层抽样的方法从中抽取n名学生进行调查.
”模式的操作又更受欢迎,即语数外三门为必考科目,然后在物理和历史中选考一门,最后从剩余的四门中选考两门.某校为了了解学生的选科情况,从高二年级的2000名学生(其中男生1100人,女生900人)中,采用分层抽样的方法从中抽取n名学生进行调查.
(1)已知抽取的n名学生中含男生110人,求n的值及抽取到的女生人数;
(2)在(1)的情况下对抽取到的n名同学“选物理”和“选历史”进行问卷调查,得到下列2×2列联表.请将列联表补充完整,并判断是否有99%的把握认为选科目与性别有关?
选物理 | 选历史 | 合计 | |
男生 | 90 | ||
女生 | 30 | ||
合计 |
(3)在(2)的条件下,从抽取的“选历史”的学生中按性别分层抽样再抽取5名,再从这5名学生中抽取2人了解选政治、地理、化学、生物的情况,求2人至少有1名男生的概率.
参考公式: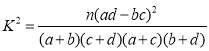 .
.
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |