题目内容
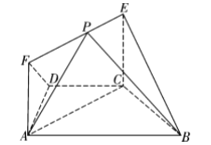
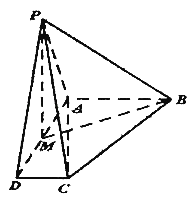
【题目】四棱锥P﹣ABCD中平面PAD⊥平面ABCD,AB∥CD,AB⊥AD,M为AD中点,PA=PD![]() ,AD=AB=2CD=2.
,AD=AB=2CD=2.
(1)求证:平面PMB⊥平面PAC;
(2)求二面角A﹣PC﹣D的余弦值.
【答案】(1)证明见详解;(2)![]()
【解析】
(1)由直线![]() 垂直于
垂直于![]() ,可得线面垂直,再由线面垂直推证面面垂直即可;
,可得线面垂直,再由线面垂直推证面面垂直即可;
(2)以![]() 为坐标原点,建立空间直角坐标系,通过求解两平面法向量的夹角,从而求得对应二面角的余弦值.
为坐标原点,建立空间直角坐标系,通过求解两平面法向量的夹角,从而求得对应二面角的余弦值.
(1)证明:∵PA=PD,M为AD中点,
∴PM⊥AD,
又平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PM⊥平面ABCD,
又因为![]() 平面
平面![]() ,
,
故![]() .
.
由已知可得,tan![]() ,
,
∴∠ABM=∠DAC,
又∵![]() ,
,
∴![]() ,
,
∴MB⊥AC,
又![]() 平面
平面![]() ,
,
故可得![]() 平面
平面![]() ,
,
又![]() 平面
平面![]()
∴平面PMB⊥平面PAC,即证.
(2)以M为坐标原点,分别以MD,MP为x轴与z轴,
建立空间直角坐标系,如下图所示:
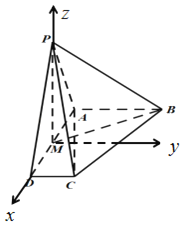
则A(﹣1,0,0),D(1,0,0),C(1,1,0),P(0,0,2).
设平面PAC的一个法向量为![]() .
.
![]() .
.
由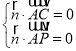 ,可得
,可得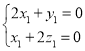 ,
,
令z1=1,得![]()
![]() ;
;
设平面PDC的一个法向量![]() ,
,
![]()
由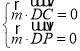 ,可得
,可得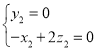 ,
,
取z2=1,得![]()
![]() .
.
设所求二面角为θ,又![]() 为锐二面角,
为锐二面角,
故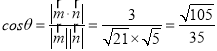 .
.
二面角A﹣PC﹣D的余弦值为![]() .
.

练习册系列答案
相关题目