题目内容
(本小题满分12分)
已知m=(cosωx+sinωx,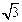 cosωx),n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m·n,且f(x)的对称中心到f(x)的对称轴的最近距离不小于
cosωx),n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m·n,且f(x)的对称中心到f(x)的对称轴的最近距离不小于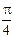 .
.
(I)求ω的取值范围;
(II)在△ABC中,a,b,c分别是内角A,B,C的对边,且a=1,b+c=2, 当ω取最大值时,f(A)=1,求△ABC的面积.
当ω取最大值时,f(A)=1,求△ABC的面积.
已知m=(cosωx+sinωx,
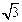 cosωx),n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m·n,且f(x)的对称中心到f(x)的对称轴的最近距离不小于
cosωx),n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m·n,且f(x)的对称中心到f(x)的对称轴的最近距离不小于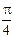 .
.(I)求ω的取值范围;
(II)在△ABC中,a,b,c分别是内角A,B,C的对边,且a=1,b+c=2,
 当ω取最大值时,f(A)=1,求△ABC的面积.
当ω取最大值时,f(A)=1,求△ABC的面积.(I)0<ω≤1
(II)S△ABC=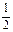 bc·sinA=
bc·sinA=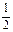 ×1·sin
×1·sin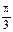 =
=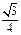
(II)S△ABC=
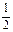 bc·sinA=
bc·sinA=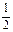 ×1·sin
×1·sin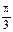 =
=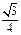
简解:( I)f(x)=2sin(2ω
I)f(x)=2sin(2ω x+
x+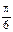 ),
),
x2-x1≥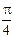 ,而 4(x2-x1)=
,而 4(x2-x1)=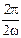 ,
,
∴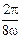 ≥
≥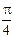
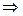 0<ω≤1 .
0<ω≤1 .
(II)∵ f(A )=1
)=1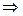 sin(2A+
sin(2A+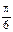 )=
)=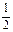 ,∵
,∵ 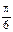 <2A+
<2A+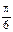 <
<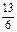 π, ∴ 2A+
π, ∴ 2A+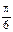 =
=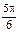
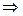 A=
A=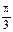 ,
,
12=b2+c2-2bccos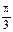 =(b+c)2-3bc,
=(b+c)2-3bc,
又b+c=2,∴ bc=1, ∴ S△ABC=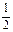 bc·sinA=
bc·sinA=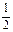 ×1·sin
×1·sin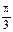 =
=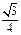
 I)f(x)=2sin(2ω
I)f(x)=2sin(2ω x+
x+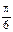 ),
),x2-x1≥
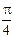 ,而 4(x2-x1)=
,而 4(x2-x1)=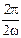 ,
,∴
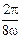 ≥
≥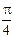
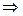 0<ω≤1 .
0<ω≤1 .
|
 )=1
)=1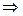 sin(2A+
sin(2A+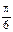 )=
)=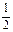 ,∵
,∵ 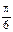 <2A+
<2A+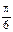 <
<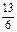 π, ∴ 2A+
π, ∴ 2A+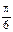 =
=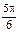
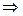 A=
A=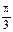 ,
,12=b2+c2-2bccos
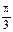 =(b+c)2-3bc,
=(b+c)2-3bc,
又b+c=2,∴ bc=1, ∴ S△ABC=
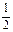 bc·sinA=
bc·sinA=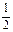 ×1·sin
×1·sin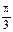 =
=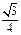

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
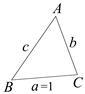
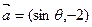 与
与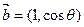 互相垂直,其中
互相垂直,其中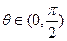 .
.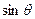 和
和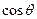 的值;
的值;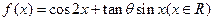 的值域。
的值域。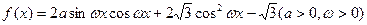 的最大值为
的最大值为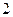 ,
,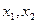 是集合
是集合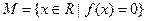 中的任意两个元素,且|
中的任意两个元素,且|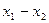 |的最小值为
|的最小值为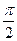 。
。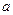 ,
,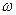 的值;
的值;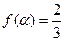 ,求
,求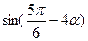 的值
的值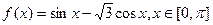 的单调减区间为 。
的单调减区间为 。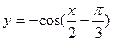 的单调递增区间是 ( )
的单调递增区间是 ( )



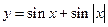 的值域
的值域 是 ( )
是 ( ) 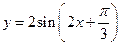 的图象是:
的图象是: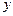 轴成轴对称
轴成轴对称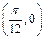 成中心对称
成中心对称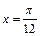 成轴对称
成轴对称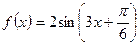 的最小正周期
的最小正周期
 的单调增区间为 ( )
的单调增区间为 ( )
 B
B 

