题目内容
1.f(x)=|x2-a|+$\frac{a}{{x}^{2}}$对一切x≠0,不等式f(x)≥1恒成立,求a的范围.分析 分x2≥a和x2<a去绝对值,由不等式f(x)≥1恒成立,令t=x2(t>0)换元后转化为二次不等式恒成立问题,然后运用三个二次的结合化为关于a的不等式组求解a的取值范围.
解答 解:若x2≥a,则f(x)=|x2-a|+$\frac{a}{{x}^{2}}$=${x}^{2}-a+\frac{a}{{x}^{2}}$,
由不等式f(x)≥1恒成立,得${x}^{2}-a+\frac{a}{{x}^{2}}≥1$恒成立,
即x4-(a+1)x2+a≥0恒成立.
令t=x2(t>0),
则t2-(a+1)t+a≥0(t>0)恒成立.
∴$\left\{\begin{array}{l}{\frac{a+1}{2}≥0}\\{(a+1)^{2}-4a≤0}\end{array}\right.$①,或$\left\{\begin{array}{l}{\frac{a+1}{2}<0}\\{a≥0}\end{array}\right.$②,
解①得:a=1,解②得a∈∅.
又a≤x2=t,∴a≤0.
故a∈∅;
若x2<a,则f(x)=|x2-a|+$\frac{a}{{x}^{2}}$=$a-{x}^{2}+\frac{a}{{x}^{2}}$,
由不等式f(x)≥1恒成立,得$a-{x}^{2}+\frac{a}{{x}^{2}}$≥1恒成立,
即x4-(a-1)x2+a≤0恒成立.
令t=x2(t>0),
则t2-(a-1)t+a≤0(t>0)恒成立.
此时显然不成立.
综上,使f(x)=|x2-a|+$\frac{a}{{x}^{2}}$,对一切x≠0,不等式f(x)≥1恒成立的实数不存在.
点评 本题考查了函数恒成立问题,考查了分类讨论的数学思想方法,训练了利用“三个二次结合”求解二次函数根的分布问题,是中高档题.

 如图,在△ABC中,已知点D在BC边上,cos∠ADC=$\frac{\sqrt{2}}{3}$,cos∠BAD=$\frac{\sqrt{3}}{3}$,AD=2,则BA的长为( )
如图,在△ABC中,已知点D在BC边上,cos∠ADC=$\frac{\sqrt{2}}{3}$,cos∠BAD=$\frac{\sqrt{3}}{3}$,AD=2,则BA的长为( )| A. | $\frac{14\sqrt{3}+4\sqrt{21}}{3}$ | B. | 7$\sqrt{3}$+4 | C. | $\sqrt{3}$+4$\sqrt{7}$ | D. | 7+4$\sqrt{7}$ |
| A. | 1+i | B. | -1+i | C. | 1-i | D. | -1-i |
 已知圆F1:(x+1)2+y2=8,点F2(1,0),点Q在圆F1上运动,QF2的垂直平分线交QF1于点P.
已知圆F1:(x+1)2+y2=8,点F2(1,0),点Q在圆F1上运动,QF2的垂直平分线交QF1于点P.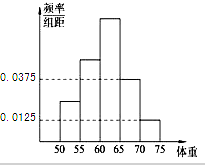 某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.
某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.