题目内容
18.已知f(x)=2sin(2x+$\frac{π}{6}$),若f(α)=$\frac{2}{3}$,α∈(0,$\frac{π}{8}$),求cos2α分析 利用f(α)=$\frac{2}{3}$,α∈(0,$\frac{π}{8}$),以及同角三角函数的基本关系式,得到余弦函数值,然后求解所求表达式.
解答 解:f(x)=2sin(2x+$\frac{π}{6}$),若f(α)=$\frac{2}{3}$,α∈(0,$\frac{π}{8}$),
所以2sin(2α+$\frac{π}{6}$)=$\frac{2}{3}$,α∈(0,$\frac{π}{8}$),
可得cos(2α+$\frac{π}{6}$)=$\frac{2\sqrt{2}}{3}$.
cos2α=cos(2α$+\frac{π}{6}-\frac{π}{6}$)=cos$\frac{π}{6}$cos(2α+$\frac{π}{6}$)+sin(2α+$\frac{π}{6}$)sin$\frac{π}{6}$=$\frac{\sqrt{3}}{2}×\frac{2\sqrt{2}}{3}+\frac{1}{2}×\frac{1}{3}$=$\frac{1+2\sqrt{6}}{6}$
点评 本题考查了二倍角的余弦,解题过程中要注意根据角的范围判断角的符号,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
3.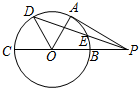 如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )
如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )
 如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )
如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )| A. | $\frac{{\sqrt{7}}}{7}$ | B. | $\frac{{3\sqrt{7}}}{7}$ | C. | $\frac{{5\sqrt{7}}}{7}$ | D. | $\sqrt{7}$ |
7.已知单位向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$-k$\overrightarrow{b}$|=$\sqrt{3}$|k$\overrightarrow{a}$+$\overrightarrow{b}$|,其中k>0,则下列与向量$\overrightarrow{b}$垂直的向量可以是( )
| A. | 6$\overrightarrow{a}$+2$\overrightarrow{b}$ | B. | $\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$ | D. | $\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$ |
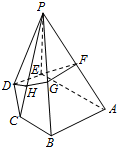 如图所示,在五棱锥P-ABCDE中,PE⊥平面ABCDE,DE⊥AE,AB∥DE,BC∥AE.AE=AB=PE=2DE=2BC,F为棱PA的中点,过D、E、F的平面α与棱PB、PC分别交于点G、H.
如图所示,在五棱锥P-ABCDE中,PE⊥平面ABCDE,DE⊥AE,AB∥DE,BC∥AE.AE=AB=PE=2DE=2BC,F为棱PA的中点,过D、E、F的平面α与棱PB、PC分别交于点G、H. 如图,△ABC内接与圆O,AD平分∠BAC交直线BC于点E,交圆O于点D.
如图,△ABC内接与圆O,AD平分∠BAC交直线BC于点E,交圆O于点D. 如图所示,在三棱锥D-ABC中,AB=BC=CD=1,AC=$\sqrt{3}$,平面ACD⊥平面ABC,∠BCD=90°
如图所示,在三棱锥D-ABC中,AB=BC=CD=1,AC=$\sqrt{3}$,平面ACD⊥平面ABC,∠BCD=90°