题目内容
1.设a为非负实数,函数f(x)=x|x-a|-a.(1)当a=2时,求函数的单调区间;
(2)求方程f(x)=0的根.
分析 (1)把函数的解析式写成分段函数的形式,画出函数的图象,数形结合求得函数的单调区间.
(2)化简函数的解析式,利用二次函数的性质,分类讨论求得函数y=x|x-a|的图象和直线y=a交点的横坐标,可得方程f(x)=0的根.
解答 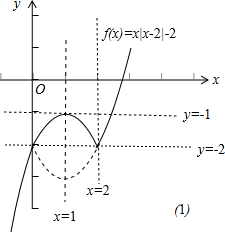 解:(1)当a=2时,函数f(x)=x|x-a|-a=x|x-2|-2=$\left\{\begin{array}{l}{x(x-2)-2,x≥2}\\{x(2-x)-2,x<2}\end{array}\right.$,
解:(1)当a=2时,函数f(x)=x|x-a|-a=x|x-2|-2=$\left\{\begin{array}{l}{x(x-2)-2,x≥2}\\{x(2-x)-2,x<2}\end{array}\right.$,
它的图象如图所示:
结合函数f(x)的图象,可得它的增区间为(-∞,1]、
[2,+∞);
它的减区间为(1,2).
(2)方程f(x)=0的根,即函数f(x)=x|x-a|-a=$\left\{\begin{array}{l}{{x}^{2}-ax-a,x≥a}\\{{-x}^{2}+ax-a,x<a}\end{array}\right.$ 的零点,
即函数y=x|x-a|的图象和直线y=a交点的横坐标.
当x≥a时,二次函数f(x)=${(x-\frac{a}{2})}^{2}$-$\frac{{a}^{2}}{4}$-a 的图象的对称轴为x=$\frac{a}{2}$<a,
f(x)在(a,+∞)上单调递增,f(a)<0.
当x<a时,二次函数f(x)=-${(x-\frac{a}{2})}^{2}$+$\frac{{a}^{2}}{4}$-a 的图象的对称轴为x=$\frac{a}{2}$<a,f(x)在($\frac{a}{2}$,a)上单调递减,
在(-∞,$\frac{a}{2}$)上单调递增,故f(x)的极大值为f($\frac{a}{2}$)=$\frac{{a}^{2}}{4}$-a.
当f($\frac{a}{2}$)<0,即0<a<4,f(x)的图象和x轴有唯一交点,
由x2-ax-a=0,求得 x=$\frac{a+\sqrt{{a}^{2}+4a}}{2}$ 或x=$\frac{a-\sqrt{{a}^{2}+4a}}{2}$(舍去).
当f($\frac{a}{2}$)=0,即a=4,f(x)的图象和x轴有2个交点,x1=2,x2=2+2$\sqrt{2}$.
当f($\frac{a}{2}$)>0,即 a>4,f(x)的图象和x轴有3个交点,由-x2+ax-a=0,求得 x=$\frac{a±\sqrt{{a}^{2}+4a}}{2}$,
此时,函数fx)的零点为$\frac{a±\sqrt{{a}^{2}+4a}}{2}$ 和$\frac{a+\sqrt{{a}^{2}+4a}}{2}$.
综上可得,当a=0时,函数的零点为0;当0<a<4时,f(x)的零点为$\frac{a+\sqrt{{a}^{2}+4a}}{2}$;
当a=4时,f(x)的零点为2和2+2$\sqrt{2}$;
当a>4 时,函数fx)的零点为$\frac{a-\sqrt{{a}^{2}+4a}}{2}$ 和$\frac{a+\sqrt{{a}^{2}+4a}}{2}$.
点评 本题主要考查函数的单调性以及函数的零点问题,体现了转化、分类讨论的数学思想,属于中档题.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案| A. | 10 | B. | 12 | C. | 20 | D. | 22 |
| A. | 100,0.2 | B. | 200,0.4 | C. | 100,0.8 | D. | 200,0.6 |
| 年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)预测该地区2016年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\hat b=\frac{{\sum_{i=1}^n{({t_i}-\bar\overline{t})({y_i}-\bar\overline{y})}}}{{\sum_{i=1}^n{{{({t_i}-\bar\overline{t})}^2}}}}$,$\hat a=\bar\overline{y}-\hat b\bar\overline{t}$.
| A. | 模型1 | B. | 模型2 | C. | 模型3 | D. | 模型4 |
| A. | $\frac{2\sqrt{a}}{a}$ | B. | $\frac{\sqrt{a}}{a}$ | C. | $\frac{1}{a}$ | D. | $\frac{2}{a}$ |