题目内容
11.已知函数y=f(x)是R上的奇函数,且x>0时,f(x)=lg(x),若g(x)=sinπx,则函数y=f(x-2)与y=g(x)图象所有公共点的横坐标之和为( )| A. | 10 | B. | 12 | C. | 20 | D. | 22 |
分析 由已知中函数y=f(x)是R上的奇函数,且x>0时,f(x)=lg(x),在同一坐标系中画出函数y=f(x-2)与y=g(x)图象,结合函数图象的对称性,可得答案.
解答 解:由已知中函数y=f(x)是R上的奇函数,且x>0时,f(x)=lg(x),
故函数y=f(x)的图象如下图所示: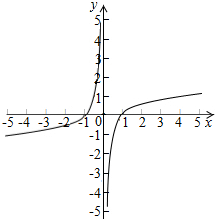
在同一坐标系中画出函数y=f(x-2)与y=g(x)图象,如下图所示: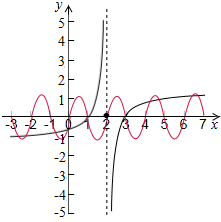
结合函数图象可得:函数y=f(x-2)与y=g(x)图象共有十一个交点,
且这些交点有十组两两关于(2,0)点对称,另外一个就是(2,0)点,
故函数y=f(x-2)与y=g(x)图象所有公共点的横坐标之和为22,
故选:D
点评 发现两个图象公共的对称中心是解决本题的入口,画出函数y=f(x-2)的图象是本题的难点所在.

练习册系列答案
相关题目
2.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=bx+a;
$\left\{\begin{array}{l}{b=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{a=\widehat{y}-b\overline{x}}\end{array}\right.$.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=bx+a;
$\left\{\begin{array}{l}{b=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{a=\widehat{y}-b\overline{x}}\end{array}\right.$.