Question

【题目】设函数，其中[x]表示不超过的最大整数，如[-1,2]=-2,[1,2]=1,[1]=1，若f(x)=kx+k有三个不同的根，则实数k的取值范围是（ ）
A.
B.
C.
D.

Answer 1

【答案】D
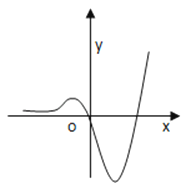
【解析】若f（x)=kx+k有三个不同的根，则函数y=f（x)的图象与y=kx+k的图象有三个交点，我们画出函数的图象，结合y=kx+k的图象恒过（-1，0)点，数形结合，易分析出k的取值范围．
∵
∴函数的图象如下图所示：

∵y=kx+k=k（x+1)，故函数图象一定过（-1，0)点
若f（x)=kx+k有三个不同的根，
则y=kx+k与y=f（x)的图象有三个交点
当y=kx+k过（2，1)点是k= ，
当y=kx+k过（3，1)点是k= ，
故f（x)=kx+k有三个不同的根，则实数k的取值范围是[ ， )
故选D