ЬтФПФкШн
ЁОЬтФПЁПЮЊСЫШУЙлЩЭгЮЭцИќБуНнЪцЪЪЃЌГЃжнПжСњдАЭЦГіСЫДњВНЙЄОпзтгУЗўЮё.вбжЊгаНХЬЄздааГЕ![]() гыЕчЖЏздааГЕ
гыЕчЖЏздааГЕ![]() СНжжГЕаЭЃЌВЩгУЗжЖЮМЦЗбЕФЗНЪНзтгУ.
СНжжГЕаЭЃЌВЩгУЗжЖЮМЦЗбЕФЗНЪНзтгУ.![]() аЭГЕУП
аЭГЕУП![]() ЗжжгЪеЗб
ЗжжгЪеЗб![]() дЊЃЈВЛзу
дЊЃЈВЛзу![]() ЗжжгЕФВПЗжАД
ЗжжгЕФВПЗжАД![]() ЗжжгМЦЫуЃЉЃЌ
ЗжжгМЦЫуЃЉЃЌ![]() аЭГЕУП
аЭГЕУП![]() ЗжжгЪеЗб
ЗжжгЪеЗб![]() дЊЃЈВЛзу
дЊЃЈВЛзу![]() ЗжжгЕФВПЗжАД
ЗжжгЕФВПЗжАД![]() ЗжжгМЦЫуЃЉЃЌЯжгаМзввБћЖЁЫФШЫЃЌЗжБ№ЯрЛЅЖРСЂЕиЕНзтГЕЕузтГЕЦяааЃЈИїзтвЛГЕвЛДЮЃЉЃЌЩшМзввБћЖЁВЛГЌЙ§
ЗжжгМЦЫуЃЉЃЌЯжгаМзввБћЖЁЫФШЫЃЌЗжБ№ЯрЛЅЖРСЂЕиЕНзтГЕЕузтГЕЦяааЃЈИїзтвЛГЕвЛДЮЃЉЃЌЩшМзввБћЖЁВЛГЌЙ§![]() ЗжжгЛЙГЕЕФИХТЪЗжБ№ЮЊ
ЗжжгЛЙГЕЕФИХТЪЗжБ№ЮЊ![]() ЃЌВЂЧвЫФИіШЫУПШЫзтГЕЖМВЛЛсГЌЙ§
ЃЌВЂЧвЫФИіШЫУПШЫзтГЕЖМВЛЛсГЌЙ§![]() ЗжжгЃЌМзввБћОљзтгУ
ЗжжгЃЌМзввБћОљзтгУ![]() аЭГЕЃЌЖЁзтгУ
аЭГЕЃЌЖЁзтгУ![]() аЭГЕЃЎ
аЭГЕЃЎ
ЃЈ1ЃЉЧѓМзввБћЖЁЫФШЫЫљИЖЕФЗбгУжЎКЭЮЊ25дЊЕФИХТЪЃЛ
ЃЈ2ЃЉЧѓМзввБћШ§ШЫЫљИЖЕФЗбгУжЎКЭЕШгкЖЁЫљИЖЕФЗбгУЕФИХТЪЃЛ
ЃЈ3ЃЉЩшМзввБћЖЁЫФШЫЫљИЖЗбгУжЎКЭЮЊЫцЛњБфСП![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФИХТЪЗжВМКЭЪ§бЇЦкЭћЃЎ
ЕФИХТЪЗжВМКЭЪ§бЇЦкЭћЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉЁАМзввБћЖЁЫФШЫЫљИЖЕФЗбгУжЎКЭЮЊ25дЊЁБЃЌ МД4ШЫОљВЛГЌЙ§30ЗжжгЁЃ
ЃЈ2ЃЉМДЖЁИЖ20дЊЃЌМзввБћШ§ШЫжагаЧвжЛгавЛШЫИЖ10 ЃЌЦфгр2ШЫИЖ5ЃЌЗж3жжЧщПіЁЃгУЯрЛЅЖРСЂЪТМўЭЌЪБЗЂЩњИХТЪЙЋЪНгыЛЅГтЪТМўЕФКЭЪТМўИХТЪЙЋЪНПЩЧѓНтЁЃЃЈ3ЃЉИљОнЗжРрПЩжЊЫцЛњБфСП![]() ЕФЫљгаШЁжЕЮЊ25ЃЌ30ЃЌ35ЃЌ40ЃЌ45ЃЌ50,ЧѓГіИХТЪМАЦкЭћЁЃ
ЕФЫљгаШЁжЕЮЊ25ЃЌ30ЃЌ35ЃЌ40ЃЌ45ЃЌ50,ЧѓГіИХТЪМАЦкЭћЁЃ
ЃЈ1ЃЉМЧЁАМзввБћЖЁЫФШЫЫљИЖЕФЗбгУжЎКЭЮЊ25дЊЁБЮЊЪТМў![]() ЃЌМД4ШЫОљВЛГЌЙ§30ЗжжгЃЌ
ЃЌМД4ШЫОљВЛГЌЙ§30ЗжжгЃЌ
дђ![]()
![]() .
.
Д№ЃКЧѓМзввБћЖЁЫФШЫЫљИЖЕФЗбгУжЎКЭЮЊ25дЊЕФИХТЪЪЧ![]()
ЃЈ2ЃЉгЩЬтвтЃЌМзввБћЖЁдк![]() ЗжжгвдЩЯЧвВЛГЌЙ§
ЗжжгвдЩЯЧвВЛГЌЙ§![]() ЗжжгЛЙГЕЕФИХТЪЗжБ№ЮЊ
ЗжжгЛЙГЕЕФИХТЪЗжБ№ЮЊ![]() ЃЌ
ЃЌ
ЩшЁАМзввБћШ§ШЫЫљИЖЗбгУжЎКЭЕШгкЖЁЫљИЖЗбгУЁБЮЊЪТМў![]() ЃЌ
ЃЌ
дђ![]()
![]()
Д№ЃКМзввБћШ§ШЫЫљИЖЕФЗбгУжЎКЭЕШгкЖЁЫљИЖЕФЗбгУЕФИХТЪЪЧ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЂйШєЁА4ШЫОљВЛГЌЙ§30ЗжжгЁБДЫЪБЫцЛњБфСП![]() ЕФжЕЮЊ25ЃЌМДЮЊЪТМў
ЕФжЕЮЊ25ЃЌМДЮЊЪТМў![]() ЃЌгЩЃЈ1ЃЉЫљвд
ЃЌгЩЃЈ1ЃЉЫљвд![]() .
.
ЂкМЧЁА4ШЫжаНігавЛШЫГЌЙ§30ЗжжгЁБЮЊЪТМў![]() ЃЌЪТМў
ЃЌЪТМў![]() гжЗжГЩСНжжЧщПіЁАГЌЙ§30ЗжжгЕФетвЛШЫЪЧМзввБћжаЕФвЛИіЁБКЭЁАГЌЙ§30ЗжжгЕФетвЛШЫЪЧЖЁЁБЃЌЗжБ№НЋЩЯЪіСНжжЧщПіМЧЮЊ
гжЗжГЩСНжжЧщПіЁАГЌЙ§30ЗжжгЕФетвЛШЫЪЧМзввБћжаЕФвЛИіЁБКЭЁАГЌЙ§30ЗжжгЕФетвЛШЫЪЧЖЁЁБЃЌЗжБ№НЋЩЯЪіСНжжЧщПіМЧЮЊ
ЪТМў![]() КЭ
КЭ![]() .
.
i.ЪТМў![]() ЖдгІЕФ
ЖдгІЕФ![]() ЕФжЕЮЊ30ЃЌДЫЪБ
ЕФжЕЮЊ30ЃЌДЫЪБ![]() ЃЛ
ЃЛ
ii.ЪТМў![]() ЖдгІЕФ
ЖдгІЕФ![]() ЕФжЕЮЊ35ЃЌДЫЪБ
ЕФжЕЮЊ35ЃЌДЫЪБ![]() .
.
ЂлМЧЁА4ШЫжаНігаСНШЫГЌЙ§30ЗжжгЁБЮЊЪТМў![]() ЃЌЪТМў
ЃЌЪТМў![]() гжЗжГЩСНжжЧщПіЁАГЌЙ§30ЗжжгЕФСНШЫЪЧМзввБћжаЕФСНИіЁБКЭЁАГЌЙ§30ЗжжгЕФСНШЫЪЧМзввБћжаЕФвЛИіКЭЖЁЁБЃЌЗжБ№НЋЩЯЪіСНжжЧщПіМЧЮЊЪТМў
гжЗжГЩСНжжЧщПіЁАГЌЙ§30ЗжжгЕФСНШЫЪЧМзввБћжаЕФСНИіЁБКЭЁАГЌЙ§30ЗжжгЕФСНШЫЪЧМзввБћжаЕФвЛИіКЭЖЁЁБЃЌЗжБ№НЋЩЯЪіСНжжЧщПіМЧЮЊЪТМў![]() КЭ
КЭ![]() .
.
i.ЪТМў![]() ЖдгІЕФ
ЖдгІЕФ![]() ЕФжЕЮЊ35ЃЌДЫЪБ
ЕФжЕЮЊ35ЃЌДЫЪБ![]() ЃЛ
ЃЛ
i.ЪТМў![]() ЖдгІЕФ
ЖдгІЕФ![]() ЕФжЕЮЊ40ЃЌДЫЪБ
ЕФжЕЮЊ40ЃЌДЫЪБ![]()
ЂмМЧЁА4ШЫжаНігаШ§ШЫГЌЙ§30ЗжжгЁБЮЊЪТМў![]() ЃЌЪТМў
ЃЌЪТМў![]() гжЗжГЩСНжжЧщПіЁАГЌЙ§30ЗжжгЕФШ§ШЫЪЧМзввБћЁБКЭЁАГЌЙ§30ЗжжгЕФШ§ШЫЪЧМзввБћжаЕФСНИіКЭЖЁЁБЃЌЗжБ№НЋЩЯЪіСНжжЧщПіМЧЮЊЪТМў
гжЗжГЩСНжжЧщПіЁАГЌЙ§30ЗжжгЕФШ§ШЫЪЧМзввБћЁБКЭЁАГЌЙ§30ЗжжгЕФШ§ШЫЪЧМзввБћжаЕФСНИіКЭЖЁЁБЃЌЗжБ№НЋЩЯЪіСНжжЧщПіМЧЮЊЪТМў![]() КЭ
КЭ![]() .
.
i.ЪТМў![]() ЖдгІЕФ
ЖдгІЕФ![]() ЕФжЕЮЊ40ЃЌДЫЪБ
ЕФжЕЮЊ40ЃЌДЫЪБ![]() ЃЛ
ЃЛ
i.ЪТМў![]() ЖдгІЕФ
ЖдгІЕФ![]() ЕФжЕЮЊ45ЃЌДЫЪБ
ЕФжЕЮЊ45ЃЌДЫЪБ![]()
![]() .
.
ЂнМЧЁА4ШЫОљГЌЙ§30ЗжжгЁБЮЊЪТМў![]() ЃЌдђЫцЛњБфСП
ЃЌдђЫцЛњБфСП![]() ЕФжЕЮЊ50ЃЌ
ЕФжЕЮЊ50ЃЌ
ДЫЪБ![]()
![]() ЃЛ
ЃЛ
злЩЯЃКЫцЛњБфСП![]() ЕФЫљгаШЁжЕЮЊ25ЃЌ30ЃЌ35ЃЌ40ЃЌ45ЃЌ50ЃЌЧв
ЕФЫљгаШЁжЕЮЊ25ЃЌ30ЃЌ35ЃЌ40ЃЌ45ЃЌ50ЃЌЧв
![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ
ЫљвдМзввБћЖЁЫФШЫЫљИЖЗбгУжЎКЭЕФЗжБ№ЮЊ
| 25 | 30 | 35 | 40 | 45 | 50 |
|
|
|
|
|
|
|
Ыљвд![]()
![]() .
.
Д№ЃКМзввБћЖЁЫФШЫЫљИЖЗбгУжЎКЭ![]() ЕФЪ§бЇЦкЭћЮЊ
ЕФЪ§бЇЦкЭћЮЊ![]() .
.

ЁОЬтФПЁПФГГЕМфЮЊСЫЙцЖЈЙЄЪБЖЈЖюЃЌашвЊШЗЖЈМгЙЄСуМўЫљЛЈЗбЕФЪБМфЃЌЮЊДЫзїСЫЫФДЮЪдбщЃЌЕУЕНЕФЪ§ОнШчЯТЃК
СуМўЕФИіЪ§ | 2 | 3 | 4 | 5 |
МгЙЄЕФЪБМф | 2.5 | 3 | 4 | 4.5 |
ЃЈЂёЃЉдкИјЖЈЕФзјБъЯЕжаЛГіБэжаЪ§ОнЕФЩЂЕуЭМЃЛ

ЃЈЂђЃЉЪдЖд![]() гы
гы![]() ЕФЙиЯЕНјааЯрЙиадМьбщ,Шч
ЕФЙиЯЕНјааЯрЙиадМьбщ,Шч![]() гы
гы![]() ОпгаЯпадЯрЙиЙиЯЕ,ЧѓГі
ОпгаЯпадЯрЙиЙиЯЕ,ЧѓГі![]() Жд
Жд![]() ЕФЛиЙщжБЯпЗНГЬЃЛ
ЕФЛиЙщжБЯпЗНГЬЃЛ
ЃЈЂѓЃЉЪддЄВтМгЙЄ![]() ИіСуМўашвЊЖрЩйЪБМфЃП
ИіСуМўашвЊЖрЩйЪБМфЃП
ВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() .
.
ИНЃК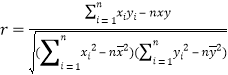 )ЃЛ
)ЃЛ ,
, ![]() ЃЛ
ЃЛ
ЯрЙиадМьбщЕФСйНчжЕБэ
n-2 | аЁИХТЪ | n-2 | аЁИХТЪ | n-2 | аЁИХТЪ | |||
0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | |||
1 | 0.997 | 1 | 4 | 0.811 | 0.917 | 7 | 0.666 | 0.798 |
2 | 0.950 | 0.990 | 5 | 0.754 | 0.874 | 8 | 0.632 | 0.765 |
3 | 0.878 | 0.959 | 6 | 0.707 | 0.834 | 9 | 0.602 | 0.735 |
зЂЃКБэжаЕФnЮЊЪ§ОнЕФзщЪ§