题目内容
【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,
且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1
,AB=2,PA=1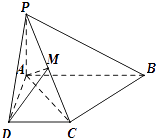
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥C﹣MAD的体积.
【答案】
(1)证明:∵底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,
∴AB∥CD,
又AB平面PCD,CD平面PCD,
∴AB∥平面PCD
(2)证明:∵∠ABC=45°,CB= ![]() ,AB=2,
,AB=2,
∴AC2=AB2+BC2﹣2ABBCcos45°= ![]() =2.
=2.
则AC2+BC2=AB2,∴BC⊥AC.
∵PA⊥平面ABCD,BC平面ABCD,∴PA⊥BC.
又PA∩AC=A,∴BC⊥平面PAC
(3)解:在直角梯形ABCD中,过C作CE⊥AB于点E,
则四边形ADCE为矩形,∴AE=DC,AD=EC.
在Rt△CEB中,可得BE=BCcos45°= ![]() ,
,
CE=BCsin45°= ![]() ,∴AE=AB﹣BE=2﹣1=1
,∴AE=AB﹣BE=2﹣1=1
∴S△ADC= ![]() =
= ![]() =
= ![]() .,
.,
∵M是PC的中点,∴M到平面ADC的距离是P到平面ADC距离的一半,
∴VC﹣MAD=VM﹣ACD= ![]() ×S△ACD×(
×S△ACD×( ![]() PA)=
PA)= ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.

【解析】(1)利用线面平行的判定定理证明;(2)利用勾股定理证明BC⊥AC,由PA⊥平面ABCD,可得PA⊥BC.从而可证得BC⊥平面PAC:(3)在直角梯形ABCD中,过C作CE⊥AB于点E,则四边形ADCE为矩形,AE=DC,AD=EC.求得CE,
计算△ACD的面积,根据M到平面ADC的距离是P到平面ADC距离的一半,求得棱锥的高,代入体积公式计算.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论,现从该班随机抽取5名学生在一次考试中的数学和物理成绩,如下表:
编号 成绩 | 1 | 2 | 3 | 4 | 5 |
物理( | 90 | 85 | 74 | 68 | 63 |
数学( | 130 | 125 | 110 | 95 | 90 |
(1)求数学成绩![]() 对物理成绩
对物理成绩![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到
精确到![]() ),若某位学生的物理成绩为80分,预测他的数学成绩(结果精确到个位);
),若某位学生的物理成绩为80分,预测他的数学成绩(结果精确到个位);
(2)要从抽取的这五位学生中随机选出2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率.
(参考公式: 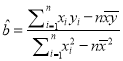 ,
, ![]() .)
.)
(参考数据: ![]() ,
, ![]() .)
.)
【题目】如表提供了甲产品的产量x(吨)与利润y(万元)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)计算相关指数R2的值,并判断线性模型拟合的效果.
参考公式: ![]() =
= 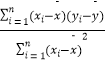 =
= 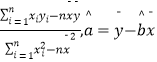 ,R2=1﹣
,R2=1﹣ 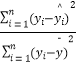 .
.