题目内容
已知双曲线
-
=1的左右焦点分别为F1、F2,O为双曲线的中心,P是双曲线右支上的点△PF1F2的内切圆的圆心为I,且圆I与x轴相切于点A,过F2作直线PI的垂线,垂足为B,则|OA|•|OB|=( )
| x2 |
| 9 |
| y2 |
| 16 |
| A、3 | B、9 | C、25 | D、16 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用切线长定理,结合双曲线的定义,把|PF1|-|PF2|=6,转化为|AF1|-|AF2|=6,从而求得点A的横坐标.再在三角形PCF2中,由题意得,它是一个等腰三角形,从而在三角形F1CF2中,利用中位线定理得出OB,从而解决问题.
解答:
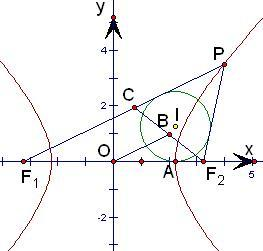 解:根据题意得F1(-5,0)、F2(5,0),
解:根据题意得F1(-5,0)、F2(5,0),
设△PF1F2的内切圆分别与PF1、PF2切于点A1、B1,与F1F2切于点A,
则|PA1|=|PB1|,|F1A1|=|F1A|,|F2B1|=|F2A|,
又点P在双曲线右支上,
所以|PF1|-|PF2|=6,故|F1A|-|F2A|=6,而|F1A|+|F2A|=10,
设A点坐标为(x,0),
则由|F1A|-|F2A|=6可得(x+5)-(5-x)=6,解得x=3,
故|OA|=3,
则△PF1F2的内切圆的圆心在直线x=3上,
在三角形PCF2中,由题意得,三角形PCF2是一个等腰三角形,PC=PF2,
∴在三角形F1CF2中,有:
|OB|=
|CF1|=
(|PF1|-|PC|)=
(|PF1|-|PF2|)=3,
∴|OA|•|OB|=9,
故选:B
 解:根据题意得F1(-5,0)、F2(5,0),
解:根据题意得F1(-5,0)、F2(5,0),设△PF1F2的内切圆分别与PF1、PF2切于点A1、B1,与F1F2切于点A,
则|PA1|=|PB1|,|F1A1|=|F1A|,|F2B1|=|F2A|,
又点P在双曲线右支上,
所以|PF1|-|PF2|=6,故|F1A|-|F2A|=6,而|F1A|+|F2A|=10,
设A点坐标为(x,0),
则由|F1A|-|F2A|=6可得(x+5)-(5-x)=6,解得x=3,
故|OA|=3,
则△PF1F2的内切圆的圆心在直线x=3上,
在三角形PCF2中,由题意得,三角形PCF2是一个等腰三角形,PC=PF2,
∴在三角形F1CF2中,有:
|OB|=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴|OA|•|OB|=9,
故选:B
点评:本题考查双曲线的定义、切线长定理.解答的关键是充分利用平面几何的性质,如三角形内心的性质等.

练习册系列答案
相关题目
若圆x2+y2+mx-
=0与直线y=-1相切,且其圆心在y轴的左侧,则m的值为( )
| 1 |
| 4 |
| A、0 | ||
| B、2 | ||
| C、1 | ||
D、
|
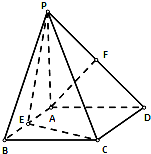 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.