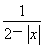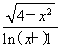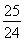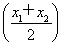题目内容
已知函数f(x)＝x2＋4ax＋2a＋6.
(1) 若f(x)的值域是[0，＋∞)，求a的值；
(2) 若函数f(x)≥0恒成立，求g(a)＝2－a|a－1|的值域．
（1）a＝－1或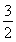
.（2）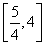
【解析】(1) ∵f(x)的值域是[0，＋∞)，即fmin(x)＝0，
∴ 
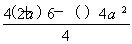＝0，∴ a＝－1或.
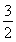(2)若函数f(x)≥0恒成立，则Δ＝(4a)2－4(2a＋6)≤0，即2a2－a－3≤0，
∴－1≤a≤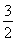
，∴g(a)＝2－a|a－1|＝
.
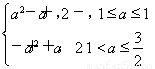当－1≤a≤1，g(a)＝a2－a＋2＝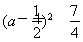
，∴ g(a)∈
；
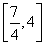当1<a≤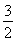
，g(a)＝－a2＋a＋2＝－
，
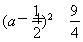∴g(a)∈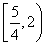
.∴函数g(a)＝2－a|a－1|的值域是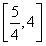
练习册系列答案
相关题目
