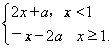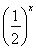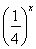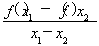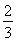题目内容

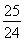已知函数f(x)＝若关于x的方程f(x)＝kx(k＞0)有且仅有四个根，其最大根为t，则函数g(t)＝t2－6t＋7的值域为________．

 

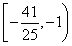
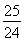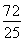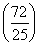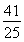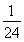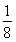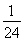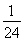【解析】在直角坐标系中分别画出函数f(x)在区间[0，2]，[2，4]，[4，6]上的三个半圆的图象，最大根t一定在区间(3，4)内，g(t)＝t2－6t＋7是二次函数，对称轴方程为4＞t＝＞3，g(t)的最小值为g＝－，直线y＝kx(k＞0)与区间[2，4]上半圆相交，与区间[4，6]上半圆相离，故<k2<，而k2＝时，直线与半圆相切，由得(1＋k2)x2－6x＋8＝0，取k2＝，得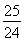x2－6x＋7＝－1，t<x，所以g(t)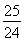＝t2－6t＋7＜－1

 

练习册系列答案
相关题目

已知f(x)是定义在R上的奇函数．当x>0时，f(x)＝x2－4x，则不等式f(x)>x的解集用区间表示为________．

 

已知函数f(x)＝x2＋4ax＋2a＋6.

(1) 若f(x)的值域是[0，＋∞)，求a的值；

(2) 若函数f(x)≥0恒成立，求g(a)＝2－a|a－1|的值域．

 

已知实数a≠0，函数f(x)＝

(1) 若a＝－3，求f(10)，f(f(10))的值；

(2) 若f(1－a)＝f(1＋a)，求a的值．

 

若函数f(x)和g(x)分别由下表给出：

x

1

2

3

4

x

1

2

3

4

f(x)

2

3

4

1

g(x)

2

1

4

3

则f(g(1))＝____________，满足g(f(x))＝1的x值是________．

 

定义在D上的函数f(x)，如果满足：对任意x∈D，存在常数M>0，都有|f(x)|≤M成立，则称f(x)是D上的有界函数，其中M称为函数f(x)的上界．已知函数f(x)＝1＋a·＋.

(1)当a＝1时，求函数f(x)在(－∞，0)上的值域，并判断函数f(x)在(－∞，0)上是否为有界函数，请说明理由；

(2)若函数f(x)在[0，＋∞)上是以3为上界的有界函数，求实数a的取值范围．

 

已知函数y＝f(x)是偶函数，对于x∈R都有f(x＋6)＝f(x)＋f(3)成立．当x1、x2∈[0，3]，且x1≠x2时，都有>0，给出下列命题：

①f(3)＝0；

②直线x＝－6是函数y＝f(x)的图象的一条对称轴；

③函数y＝f(x)在[－9，－6]上为单调增函数；

④函数y＝f(x)在[－9，9]上有4个零点．

其中正确的命题是________．(填序号)

 

我国辽东半岛普兰附近的泥炭层中，发掘出的古莲子，至今大部分还能发芽开花，这些古莲子是多少年以前的遗物呢？要测定古物的年代，可用放射性碳法．在动植物的体内都含有微量的放射性14C，动植物死亡后，停止了新陈代谢，14C不再产生，且原有的14C会自动衰变，经过5570年(叫做14C的半衰期)，它的残余量只有原始量的一半，经过科学家测定知道，若14C的原始含量为a，则经过t年后的残余量a′(与a之间满足a′＝a·e－kt)．现测得出土的古莲子中14C残余量占原量的87.9%，试推算古莲子的生活年代．

 

某一运动物体，在x(s)时离出发点的距离(单位：m)是f(x)＝x3＋x2＋2x.

(1)求在第1s内的平均速度；

(2)求在1s末的瞬时速度；

(3)经过多少时间该物体的运动速度达到14m/s?

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网