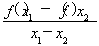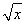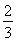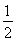题目内容
设函数f(x)=x2-(a-2)x-alnx.
(1)求函数f(x)的单调区间;
(2)若函数f(x)有两个零点,求满足条件的最小正整数a的值;
(3)若方程f(x)=c有两个不相等的实数根x1、x2,求证:f′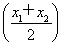 >0.
>0.
(1)单调增区间为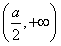 ,单调减区间为
,单调减区间为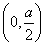 (2)3(3)见解析
(2)3(3)见解析
【解析】(1)【解析】
f′(x)=2x-(a-2)- (x>0).
(x>0).
当a≤0时,f′(x)>0,函数f(x)在(0,+∞)上单调递增,
所以函数f(x)的单调增区间为(0,+∞).
当a>0时,由f′(x)>0,得x> 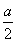 ;由f′(x)<0,得0<x<
;由f′(x)<0,得0<x< 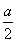 .
.
所以函数f(x)的单调增区间为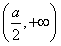 ,单调减区间为
,单调减区间为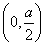 .
.
(2)【解析】
由(1)得,若函数f(x)有两个零点,则a>0,且f(x)的最小值f 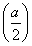 <0,即-a2+4a-4aln
<0,即-a2+4a-4aln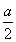 <0.因为a>0,所以a+4ln
<0.因为a>0,所以a+4ln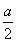 -4>0.
-4>0.
令h(a)=a+4ln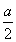 -4,显然h(a)在(0,+∞)上为增函数,且h(2)=-2<0,h(3)=4ln
-4,显然h(a)在(0,+∞)上为增函数,且h(2)=-2<0,h(3)=4ln 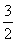 -1=ln
-1=ln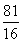 -1>0,所以存在a0∈(2,3),h(a0)=0.
-1>0,所以存在a0∈(2,3),h(a0)=0.
当a>a0时,h(a)>0;当0<a<a0时,h(a)<0.所以满足条件的最小正整数a=3.
又当a=3时,f(3)=3(2-ln3)>0,f(1)=0,所以a=3时,f(x)有两个零点.
综上所述,满足条件的最小正整数a的值为3.
(3)证明:因为x1、x2是方程f(x)=c的两个不等实根,由(1)知a>0.
不妨设0<x1<x2,则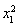 -(a-2)x1-alnx1=c,
-(a-2)x1-alnx1=c,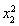 -(a-2)x2-alnx2=c.
-(a-2)x2-alnx2=c.
两式相减得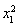 -(a-2)x1-alnx1-
-(a-2)x1-alnx1-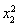 +(a-2)·x2+alnx2=0,
+(a-2)·x2+alnx2=0,
即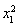 +2x1-
+2x1-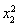 -2x2=ax1+alnx1-ax2-alnx2=a(x1+lnx1-x2-lnx2).
-2x2=ax1+alnx1-ax2-alnx2=a(x1+lnx1-x2-lnx2).
所以a=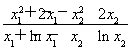 .
.
因为f′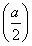 =0,当x∈
=0,当x∈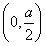 时,f′(x)<0,当x∈
时,f′(x)<0,当x∈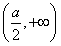 时,f′(x)>0,
时,f′(x)>0,
故只要证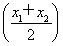 >
> 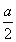 即可,即证明x1+x2>
即可,即证明x1+x2> 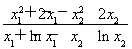 ,
,
即证明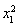 -
-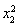 +(x1+x2)(lnx1-lnx2)<
+(x1+x2)(lnx1-lnx2)< 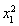 +2x1-
+2x1-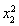 -2x2,
-2x2,
即证明ln 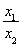 <
<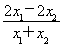 .设t=
.设t=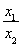 (0<t<1).
(0<t<1).
令g(t)=lnt-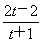 ,则g′(t)=
,则g′(t)=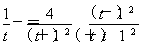 .
.
因为t>0,所以g′(t)≥0,当且仅当t=1时,g′(t)=0,
所以g(t)在(0,+∞)上是增函数.
又g(1)=0,所以当t∈(0,1),g(t)<0总成立.所以原题得证.