题目内容
【题目】已知数列{an}的前n项和 ![]() . (Ⅰ)求数列{an}的通项公式;
. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ![]() ,求数列{anbn2}的前n项和Tn .
,求数列{anbn2}的前n项和Tn .
【答案】解:(Ⅰ)因为Sn=n2+2n, 所以当n≥2时,an=Sn﹣Sn﹣1=n2+2n﹣[(n﹣1)2+2(n﹣1)]=2n+1.
当n=1时,a1=S1=12+2×1=3,满足上式.
故an=2n+1.
(Ⅱ)因为bn=2n . 所以anbn2=(2n+1)4n ,
其前n项和:Tn=34+542+743+…+(2n﹣1)4n﹣1+(2n+1)4n①
两边乘以4得:4Tn=342+543+…+(2n﹣1)4n+(2n+1)4n+1…②
由①﹣②得:﹣3Tn=34+242+243+…+24n﹣(2n+1)4n+1
= ![]()
所以Tn= ![]() .
.
【解析】(I)利用递推关系即可得出.(II)利用“错位相减法”与等比数列的求和公式即可得出.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系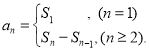 .
.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目