题目内容
【题目】已知椭圆C： 
=1（a＞b＞0）的左、右焦点分别为F1 ， F2 ， 离心率为 
．以原点为圆心，椭圆的短轴长为直径的圆与直线x﹣y+ 
=0相切．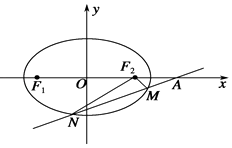 
（1）求椭圆C的方程；
（2）如图，若斜率为k（k≠0）的直线l与x轴、椭圆C顺次相交于A，M，N（A点在椭圆右顶点的右侧），且∠NF2F1=∠MF2A．求证直线l恒过定点，并求出斜率k的取值范围．
【答案】
（1）解：由椭圆C： 
=1（a＞b＞0）可知焦点在x轴上，
离心率e= 
= 
，
∴e2= 
= 
= 
，即a2=2b2．
∵以原点为圆心，椭圆的短轴长为直径的圆与直线x﹣y+ 
=0相切，
∴原点到直线x﹣y+ =0的距离为b，
b= 
= 
=1，
∴b2=1，a2=2，
∴椭圆方程为 
+y2=1
（2）解：由题意，设直线l的方程为y=kx+m（k≠0），M（x1，y1），N（x2，y2）．
由 
，整理得：（2k2+1）x2+4kmx+2m2﹣2=0．
由△=16k2m2﹣4（2k2+1）（2m2﹣2）＞0，得m2＜2k2+1，
由韦达定理可知：x1+x2=﹣ 
，x1x2= 
．
∵∠NF2F1=∠MF2A，且∠MF2A≠90°， 
+ 
=0．
又F2（1，0），
则 
+ 
=0，即 
+ 
=0，
化简得：2kx1x2+（m﹣k）（x1+x2）﹣2m=0．
将x1+x2=﹣ ，x1x2= ，代入上式，求得m=﹣2k，
∴直线l的方程为y=kx﹣2k=k（x﹣2），
∴直线过定点（2，0）．
将m=﹣2k代入m2＜2k2+1，
得4k2＜2k2+1，即k2＜ ，
又∵k≠0，
∴直线l的斜率k的取值范围是（﹣ ，0）∪（0， ）
【解析】（1）由题意可知：椭圆焦点在x轴上，离心率e= = ，求得a2=2b2 ． 由原点到直线x﹣y+ =0的距离为b，即b= = =1，即可求得2=2，即可求得椭圆的标准方程；（2）设直线l的方程为y=kx+m（k≠0），代入椭圆方程，由△＞0，求得m2＜2k2+1，由韦达定理可知：x1+x2=﹣ ，x1x2= ，∠NF2F1=∠MF2A，且∠MF2A≠90°， + =0，由直线的斜率公式，求得2kx1x2+（m﹣k）（x1+x2）﹣2m=0．即可求得m=﹣2k，代入直线方程求得y=kx﹣2k=k（x﹣2），则直线过定点（2，0），由m2＜2k2+1，即可求得斜率k的取值范围．
