题目内容
【题目】已知线段AB的端点B在圆C1：x2+（y﹣4）2=16上运动，端点A的坐标为（4，0），线段AB中点为M， （Ⅰ）试求M点的轨C2方程；
（Ⅱ）若圆C1与曲线C2交于C，D两点，试求线段CD的长．
【答案】解：（Ⅰ）设M（x，y），B（x′，y′）， 则由题意可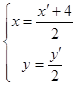得： 
，解得： 
，
∵点B在圆C1：x2+（y﹣4）2=16上，
∴（x′）2+（y′﹣4）2=16，
∴（2x﹣4）2+（2y﹣4）2=16，即（x﹣2）2+（y﹣2）2=4．
∴轨迹C2方程为（x﹣2）2+（y﹣2）2=4；
（Ⅱ）由方程组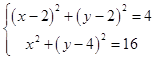 
，解得直线CD的方程为x﹣y﹣1=0，
圆C1 的圆心C1（0，4）到直线CD的距离为 
，
圆C1 的半径为4，
∴线段CD的长为 
【解析】（Ⅰ）设出M和B的坐标，由中点坐标公式把B的坐标用m的坐标表示，代入圆C1的方程得答案；（Ⅱ）求出圆C1的圆心坐标和半径，求出圆心到直线CD的距离利用勾股定理得答案．
练习册系列答案
相关题目
