题目内容
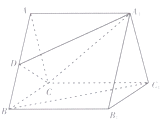
【题目】如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP. (Ⅰ)设点M为棱PD中点,求证:EM∥平面ABCD;
(Ⅱ)线段PD上是否存在一点N,使得直线BN与平面PCD所成角的正弦值等于 ![]() ?若存在,试确定点N的位置;若不存在,请说明理由.
?若存在,试确定点N的位置;若不存在,请说明理由.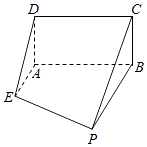
【答案】证明:(Ⅰ)∵平面ABCD⊥平面ABEP,平面ABCD∩平面ABEP=AB,BP⊥AB ∴BP⊥平面ABCD,又AB⊥BC,
∴直线BA,BP,BC两两垂直,
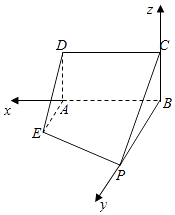
以B为原点,分别以BA,BP,BC为x轴,y轴,z轴建立如图所示的空间直角坐标系.
则P(0,2,0),B(0,0,0),D(2,0,1),E(2,1,0),C(0,0,1),∴M(1,1, ![]() ),
),
∴ ![]() =(﹣1,0,
=(﹣1,0, ![]() ),
), ![]() =(0,2,0).
=(0,2,0).
∵BP⊥平面ABCD,∴ ![]() 为平面ABCD的一个法向量,
为平面ABCD的一个法向量,
∵ ![]() =﹣1×0+0×2+
=﹣1×0+0×2+ ![]() =0,
=0,
∴ ![]() ⊥
⊥ ![]() .又EM平面ABCD,
.又EM平面ABCD,
∴EM∥平面ABCD.
(Ⅱ)解:当点N与点D重合时,直线BN与平面PCD所成角的正弦值为 ![]() .
.
理由如下:
∵ ![]() =(2,﹣2,1),
=(2,﹣2,1), ![]() =(2,0,0),
=(2,0,0),
设平面PCD的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 ![]() .
.
令y=1,得 ![]() =(0,1,2).
=(0,1,2).
假设线段PD上存在一点N,使得直线BN与平面PCD所成角α的正弦值等于 ![]() .
.
设 ![]() =λ
=λ ![]() =(2λ,﹣2λ,λ)(0≤λ≤1),∴
=(2λ,﹣2λ,λ)(0≤λ≤1),∴ ![]() =
= ![]() +
+ ![]() =(2λ,2﹣2λ,λ).
=(2λ,2﹣2λ,λ).
∴|cos< ![]() ,
, ![]() >|=
>|= ![]() =
= ![]() .
.
∴9λ2﹣8λ﹣1=0,解得λ=1或 ![]() (舍去).
(舍去).
∴当N点与D点重合时,直线BN与平面PCD所成角的正弦值等于 ![]() .
.
【解析】(I)证明BP⊥平面ABCD,以B为原点建立坐标系,则 ![]() 为平面ABCD的法向量,求出
为平面ABCD的法向量,求出 ![]() =﹣1×0+0×2+
=﹣1×0+0×2+ ![]() =0,从而有EM∥平面ABCD;(II)假设存在点N符合条件,设
=0,从而有EM∥平面ABCD;(II)假设存在点N符合条件,设 ![]() =λ
=λ ![]() ,求出
,求出 ![]() ,平面PCD的法向量
,平面PCD的法向量 ![]() 的坐标,令|cos<
的坐标,令|cos< ![]() ,
, ![]() >|=
>|= ![]() =
= ![]() 解出λ,根据λ的值得出结论.
解出λ,根据λ的值得出结论.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则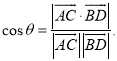 .
.

 阅读快车系列答案
阅读快车系列答案