题目内容
4.与椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1共焦点,且过点P(3$\sqrt{2}$,$\sqrt{7}$)的双曲线的方程为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{7}=1$.分析 根据椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,得到a2=25,b2=9,所以c2=a2-b2=16,再设所求双曲线方程为$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{n}$=1,(m>0,n>0).然后结合题意:双曲线与椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1共焦点,且过点P(3$\sqrt{2}$,$\sqrt{7}$),列出方程组并解之可得m=9,n=7,从而得到所求双曲线的方程.
解答 解:∵椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1中,a2=25,b2=9,
∴c2=a2-b2=16
设双曲线方程为$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{n}$=1,(m>0,n>0)
∵双曲线与椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1共焦点,且过点P(3$\sqrt{2}$,$\sqrt{7}$),
∴m+n=16且$\frac{18}{m}-\frac{7}{n}$=1,解之可得m=9,n=7,
∴双曲线方程是$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{7}=1$.
故答案为:$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{7}=1$.
点评 本题给出与已知椭圆共焦点的双曲线且经过一个已知定点,求双曲线的标准方程,着重考查了椭圆的基本概念和双曲线的简单几何性质,属于中档题.

练习册系列答案
相关题目
15.已知a,b∈R+,直线ax+by=5平分圆x2+y2-2x-4y+1=0的周长.则a2+b2的最小值为( )
| A. | 5 | B. | $\sqrt{5}$ | C. | 25 | D. | 5$\sqrt{5}$ |
19.在直角三角形ABC中,C=90°,B=30°,AB=4,M是AB的中点,将三角形ACM沿CM翻折成直二面角,则三棱锥A-CBM的外接球的表面积为( )
| A. | $\frac{52π}{3}$ | B. | $\frac{18π}{5}$ | C. | $\frac{14π}{3}$ | D. | 12π |
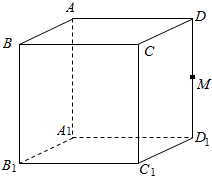 如图,M是正方体ABCD-A1B1C1D1的棱DD1的中点,给出下列命题:
如图,M是正方体ABCD-A1B1C1D1的棱DD1的中点,给出下列命题: