题目内容
9.已知圆心在第一象限的圆过点P(-4,3),圆心在直线2x-y+1=0上,且半径为5,则这个圆的方程为(x-1)2+(y-3)2=25.分析 设圆心坐标为(a,b),a>0,b>0,把圆心代入直线2x-y+1=0,再由圆心到点P的距离等于半径,列出方程组求出圆心坐标,由此能求出圆的方程.
解答 解:设圆心坐标为(a,b),a>0,b>0,
由已知得$\left\{\begin{array}{l}{2a-b+1=0}\\{\sqrt{(a+4)^{2}+(b-3)^{2}}=5}\end{array}\right.$,
解得a=1,b=3,
∴(x-1)2+(y-3)2=25.
故答案为:(x-1)2+(y-3)2=25.
点评 本题考查圆的方程的求法,是基础题,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
相关题目
14.函数y=f(x)的定义域是[0,2],则函数y=$\frac{f(2x)}{\sqrt{1-x}}$+lgx的定义域是( )
| A. | [0,1] | B. | [0,1) | C. | [0,1)∪(1,4] | D. | (0,1) |
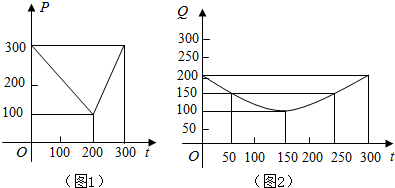 某种蔬菜基地种植西红柿由历年市场行情得知,从2月1日起的300天内,西红柿市场售价p与上市时间t的关系图是一条折线(如图(1)),种植成本Q与上市时间t的关系是一条抛物线(如图(2)).
某种蔬菜基地种植西红柿由历年市场行情得知,从2月1日起的300天内,西红柿市场售价p与上市时间t的关系图是一条折线(如图(1)),种植成本Q与上市时间t的关系是一条抛物线(如图(2)).