题目内容
15.已知a,b∈R+,直线ax+by=5平分圆x2+y2-2x-4y+1=0的周长.则a2+b2的最小值为( )| A. | 5 | B. | $\sqrt{5}$ | C. | 25 | D. | 5$\sqrt{5}$ |
分析 直线ax+by=5平分圆x2+y2-2x-4y+1=0的周长可得:直线ax+by=5经过圆心C(1,2),于是a+2b-5=0.再利用的几何意义即可得出.
解答 解:圆x2+y2-2x-4y+1=0化为(x-1)2+(y-2)2=4,圆心为C(1,2),
∵a,b∈R+,直线ax+by=5平分圆x2+y2-2x-4y+1=0的周长,
∴直线ax+by=5经过圆心C(1,2),
∴a+2b-5=0.
∴圆心到直线的距离为$\frac{|-5|}{\sqrt{1+4}}$=$\sqrt{5}$.
∴a2+b2的最小值为5.
故选:A.
点评 本题考查了圆的性质、点到直线的距离,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 如图,已知ABCD和ABEF是两个全等的矩形,M、N分别为AC、FB上的点,且AM=FN,过点M作MP∥CB,交AB于P,求证:平面MNP∥平面CEB.
如图,已知ABCD和ABEF是两个全等的矩形,M、N分别为AC、FB上的点,且AM=FN,过点M作MP∥CB,交AB于P,求证:平面MNP∥平面CEB.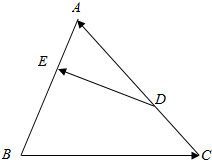 如图,在△ABC中,D、E分别为AC,AB边上的点,$\frac{CD}{DA}$=$\frac{AE}{EB}$=$\frac{1}{2}$,记$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$.求证:$\overrightarrow{DE}$=$\frac{1}{3}$($\overrightarrow{b}$-$\overrightarrow{a}$).
如图,在△ABC中,D、E分别为AC,AB边上的点,$\frac{CD}{DA}$=$\frac{AE}{EB}$=$\frac{1}{2}$,记$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$.求证:$\overrightarrow{DE}$=$\frac{1}{3}$($\overrightarrow{b}$-$\overrightarrow{a}$).