题目内容
19．在直角三角形ABC中，C=90°，B=30°，AB=4，M是AB的中点，将三角形ACM沿CM翻折成直二面角，则三棱锥A-CBM的外接球的表面积为（ ）| A． | $\frac{52π}{3}$ | B． | $\frac{18π}{5}$ | C． | $\frac{14π}{3}$ | D． | 12π |
分析 先求出△BCM的外接圆的半径，再利用勾股定理建立方程，求出球的半径，即可求出三棱锥A-CBM的外接球的表面积．
解答 解：由题意，△BCM中，BC=2$\sqrt{3}$，∠BMC=120°．
设△BCM的外接圆的半径为r，则2r=$\frac{2\sqrt{3}}{sin120°}$=4．
设球心到平面BCD的距离为d，球的半径为R，则R2=4+d2=（$\sqrt{3}$）2+（$\sqrt{3}$-d）2，
∴d=$\frac{1}{\sqrt{3}}$，R2=$\frac{13}{3}$，
∴三棱锥A-CBM的外接球的表面积为4πR2=$\frac{52π}{3}$，
故选：A．
点评 本题考查三棱锥A-CBM的外接球的表面积，考查学生的计算能力，求出球的半径，是关键．
练习册系列答案
相关题目
9．方程2$\sqrt{（x-1）^{2}+（y-1）^{2}}$=|x+y+2|表示的曲线 （ ）
| A． | 椭圆 | B． | 双曲线 | C． | 线段 | D． | 抛物线 |
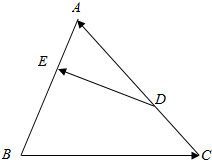如图，在△ABC中，D、E分别为AC，AB边上的点，$\frac{CD}{DA}$=$\frac{AE}{EB}$=$\frac{1}{2}$，记$\overrightarrow{BC}$=$\overrightarrow{a}$，$\overrightarrow{CA}$=$\overrightarrow{b}$．求证：$\overrightarrow{DE}$=$\frac{1}{3}$（$\overrightarrow{b}$-$\overrightarrow{a}$）．