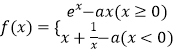题目内容
【题目】我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f（x）=anxn+an﹣1xn﹣1+…+a1x+a0的值的秦九韶算法，即将f（x）改写成如下形式：f（x）=（…（（anx+an﹣1）x+an﹣2）x+…+a1）x+a0 ， 首先计算最内层一次多项式的值，然后由内向外逐层计算一次多项式的值，这种算法至今仍是比较先进的算法，将秦九韶算法用程序框图表示如图，则在空白的执行框内应填入（ ）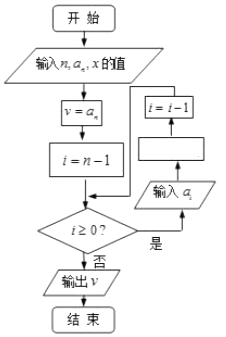
A.v=vx+ai
B.v=v（x+ai）
C.v=aix+v
D.v=ai（x+v）
【答案】A
【解析】解：秦九韶算法的过程是 
（k=1，2，…，n）这个过程用循环结构来实现，
应在题目的空白的执行框内填入v=vx+ai，
故答案为：A．
读懂程序框图，这个过程用循环结构来实现，不难得到答案.
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
