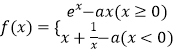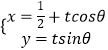题目内容
【题目】设集合U={1，2，…，100}，TU．对数列{an}（n∈N*），规定：
①若T=，则ST=0；
②若T={n1 ， n2 ， …，nk}，则ST=a 
+a 
+…+a 
．
例如：当an=2n，T={1，3，5}时，ST=a1+a3+a5=2+6+10=18．
已知等比数列{an}（n∈N*），a1=1，且当T={2，3}时，ST=12，求数列{an}的通项公式．
【答案】解：∵等比数列{an}（n∈N*），a1=1，且当T={2，3}时，ST=12，
∴a2+a3=12，即q+q2=12，
解得q=3或q=﹣4，
∴当q=3时，an=a 
=3n﹣1，
当q=﹣4时，an=a =（﹣4）n﹣1，
∴数列{an}的通项公式为 
或 
．
【解析】由题意可得当T={2，3}时，ST=12，∴a2+a3=12，即q+q2=12，
解得q=3或q=﹣4，∴当q=3时，an=a =3n﹣1，
当q=﹣4时，an=a =（﹣4）n﹣1，∴数列{an}的通项公式为 或 ．
练习册系列答案
名校课堂系列答案
相关题目
