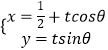题目内容
【题目】在极坐标系中,曲线C的极坐标方程为ρ=2cosθ+2sinθ(0≤θ<2π),点M(1, ![]() ),以极点O为原点,以极轴为x轴的正半轴建立平面直角坐标系.已知直线l:
),以极点O为原点,以极轴为x轴的正半轴建立平面直角坐标系.已知直线l: 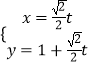 (t为参数)与曲线C交于A,B两点,且|MA|>|MB|.
(t为参数)与曲线C交于A,B两点,且|MA|>|MB|.
(1)若P(ρ,θ)为曲线C上任意一点,求ρ的最大值,并求此时点P的极坐标;
(2)求 ![]() .
.
【答案】
(1)解:曲线C的极坐标方程为ρ=2cosθ+2sinθ=2 ![]() (0≤θ<2π),
(0≤θ<2π),
当θ= ![]() 时,ρ取得最大值2
时,ρ取得最大值2 ![]() ,此时P
,此时P ![]() .
.
(2)由ρ=2cosθ+2sinθ可得:ρ2=2ρcosθ+2ρsinθ,可得直角坐标方程:x2+y2﹣2x﹣2y=0.
配方为:(x﹣1)2+(y﹣1)2=2.
点M(1, ![]() )化为(0,1),
)化为(0,1),
直线l: 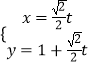 (t为参数)代入圆的方程可得:t2﹣
(t为参数)代入圆的方程可得:t2﹣ ![]() t﹣1=0,解得t=
t﹣1=0,解得t= ![]() .
.
∵|MA|>|MB|.由t的几何意义可得:|MA|= ![]() ,|MB|=
,|MB|= ![]() .
.
∴ ![]() =
= ![]() =2+
=2+ ![]() .
.
【解析】(1)对曲线C的极坐标方程进行三角恒等变换,根据正弦函数的最值可得P点的坐标;(2)将曲线C的方程化为直角坐标方程,将直线l的参数方程代入圆的方程,由t的几何意义求![]() .
.

练习册系列答案
相关题目