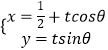题目内容
【题目】数列{an}是公差为d（d≠0）的等差数列，Sn为其前n项和，a1 ， a2 ， a5成等比数列．
（Ⅰ）证明S1 ， S3 ， S9成等比数列；
（Ⅱ）设a1=1，求 
的值．
【答案】解：（Ⅰ）证明：由题意有 
，即 
，解得d=2a1，…
又S1=a1，S3=3a1+3d=9a1，S9=9a1+36d=81a1，…
即 
，…
又∵S1，S3，S9均不为零，
所以S1，S3，S9成等比数列．…
（Ⅱ）a1=1，由（Ⅰ）可知d=2，所以an=2n﹣1，…
所以 
…
原式= 
…
=2（2+22+23+…+2n）﹣n
= 
=2n+2﹣n﹣4…
【解析】1、本题考查的是等比数列前n项和公式，由题意有 a22 = a 1 a 5 ，即 ( a1 + d ) 2 = a 1 ( a 1 + 4 d ) ，解得d=2a1，…
又S1=a1，S3=3a1+3d=9a1，S9=9a1+36d=81a1，…即 S32= S 1 S 9 ，…可得证。
2、由（1）可知d=2，所以an=2n﹣1，… ， a 2n = 2 2 n 1 …
原式= a 2+ a 2 2+ a 2 3 + a 2 n = ( 2 2 1 ) + ( 2 2 2 1 ) + ( 2 2 3 1 ) + + ( 2 2 n 1 ) …=2n+2﹣n﹣4…
练习册系列答案
阅读快车系列答案
相关题目
