题目内容
根据下列条件,求出抛物线的标准方程.
(1)过点(-3,2).
(2)焦点在x轴上,且抛物线上一点A(3,m)到焦点的距离为5.
(1)过点(-3,2).
(2)焦点在x轴上,且抛物线上一点A(3,m)到焦点的距离为5.
(1)∵抛物线过点(-3,2),
∴当焦点在x轴时设其标准方程为:y2=-2px(p>0)
∴4=-2p×(-3),
解得p=
,
∴其标准方程为y2=-
x;
当焦点在y轴时,设其标准方程为:x2=2py(p>0),
同理可得,p=
,其标准方程为x2=
y;
综上所述,过点(-3,2)的抛物线的标准方程为:y2=-
x或x2=
y;
(2)设该抛物线的标准方程为y2=2px(p>0),
则其准线方程为:x=-
,
∵抛物线上一点A(3,m)到焦点的距离为5,
∴由抛物线的定义知,3-(-
)=5,
解得:p=4,
∴抛物线的标准方程为y2=8x.
∴当焦点在x轴时设其标准方程为:y2=-2px(p>0)
∴4=-2p×(-3),
解得p=
| 2 |
| 3 |
∴其标准方程为y2=-
| 4 |
| 3 |
当焦点在y轴时,设其标准方程为:x2=2py(p>0),
同理可得,p=
| 9 |
| 4 |
| 9 |
| 2 |
综上所述,过点(-3,2)的抛物线的标准方程为:y2=-
| 4 |
| 3 |
| 9 |
| 2 |
(2)设该抛物线的标准方程为y2=2px(p>0),
则其准线方程为:x=-
| p |
| 2 |
∵抛物线上一点A(3,m)到焦点的距离为5,
∴由抛物线的定义知,3-(-
| p |
| 2 |
解得:p=4,
∴抛物线的标准方程为y2=8x.

练习册系列答案
相关题目
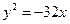 上一点到焦点的距离为
上一点到焦点的距离为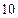 ,求该点的坐标。
,求该点的坐标。