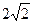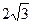题目内容
已知抛物线顶点在原点,焦点在坐标轴上,又知此抛物线上一点A(m,-3)到焦点F的距离是5,求抛物线的方程及m的值.
分三种情况加以讨论
(1)当抛物线焦点在x轴正半轴上时,设其方程为y2=2px(p>0)
代入A点坐标,得2pm=9…①
∵抛物线上一点A(m,-3)到焦点F的距离为5
∴m+
=5…②
将①②两式联解得:m=
、p=9或m=
、p=1,
相应的抛物线方程为y2=18x和y2=2x;
(2)当抛物线焦点在x轴负半轴上时,设其方程为y2=-2px(p>0)
代入A点坐标,得-2pm=9…③
∵抛物线上一点A(m,-3)到焦点F的距离为5,∴-m+
=5…④
将③④两式联解得:m=-
、p=9或m=-
、p=1,
相应的抛物线方程为y2=-18x和y2=-2x;
可得m=-
或m=
,相应的抛物线方程为y2=-18x或y2=-2x;
(3)当抛物线焦点在y轴上时,设其方程为x2=-2qy(q>0)
将点A(m,-3)代入方程,得m2=6q…③
∵抛物线上一点A(m,-3)到焦点F的距离为5
∴3+
=5解之得q=4,代入③得m=±2
此时抛物线的方程为x2=-8y,
综上所述,抛物线方程为y2=18x,m=
;或抛物线方程为y2=2x,m=
;或抛物线方程为y2=-18x,m=-
;或抛物线的方程为y2=-2x,m=
;或抛物线的方程为x2=-8y,m=±2
.
(1)当抛物线焦点在x轴正半轴上时,设其方程为y2=2px(p>0)
代入A点坐标,得2pm=9…①
∵抛物线上一点A(m,-3)到焦点F的距离为5
∴m+
| p |
| 2 |
将①②两式联解得:m=
| 1 |
| 2 |
| 9 |
| 2 |
相应的抛物线方程为y2=18x和y2=2x;
(2)当抛物线焦点在x轴负半轴上时,设其方程为y2=-2px(p>0)
代入A点坐标,得-2pm=9…③
∵抛物线上一点A(m,-3)到焦点F的距离为5,∴-m+
| p |
| 2 |
将③④两式联解得:m=-
| 1 |
| 2 |
| 9 |
| 2 |
相应的抛物线方程为y2=-18x和y2=-2x;
可得m=-
| 1 |
| 2 |
| 9 |
| 2 |
(3)当抛物线焦点在y轴上时,设其方程为x2=-2qy(q>0)
将点A(m,-3)代入方程,得m2=6q…③
∵抛物线上一点A(m,-3)到焦点F的距离为5
∴3+
| q |
| 2 |
| 6 |
此时抛物线的方程为x2=-8y,
综上所述,抛物线方程为y2=18x,m=
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 6 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 被点
被点 所平分的弦的直线方程。
所平分的弦的直线方程。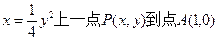 的距离为3,又点
的距离为3,又点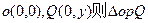 的面积为( )
的面积为( )