题目内容
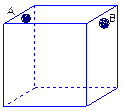
为处理含有某种杂质的污水,要制造一个底宽为2米的无盖长方体沉淀箱(如图),污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60平方米,问当a、b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?

当a=6,b=3时,经沉淀后流出的水中该杂质的质量分数最小.
解法一:设经沉淀后流出的水中该杂质的质量分数为y,则由条件y=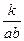 (k>0为比例系数)其中a、b满足2a+4b+2ab="60 " ①
(k>0为比例系数)其中a、b满足2a+4b+2ab="60 " ①
要求y的最小值,只须求ab的最大值.
由①(a+2)(b+1)=32(a>0,b>0)且ab=30–(a+2b)
应用重要不等式a+2b=(a+2)+(2b+2)–4≥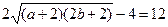
∴ab≤18,当且仅当a=2b时等号成立
将a=2b代入①得a=6,b=3.
故当且仅当a=6,b=3时,经沉淀后流出的水中该杂质的质量分数最小.
解法二:由2a+4b+2ab=60,得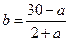 ,
,
记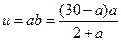 (0<a<30)则要求y的最小值只须求u的最大值.
(0<a<30)则要求y的最小值只须求u的最大值.
由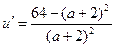 ,令u′=0得a=6
,令u′=0得a=6
且当0<a<6时,u′>0,当6<u<30时u′<0,
∴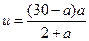 在a=6时取最大值,此时b=3.
在a=6时取最大值,此时b=3.
从而当且仅当a=6,b=3时,y=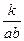 取最小值.
取最小值.
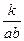 (k>0为比例系数)其中a、b满足2a+4b+2ab="60 " ①
(k>0为比例系数)其中a、b满足2a+4b+2ab="60 " ①要求y的最小值,只须求ab的最大值.
由①(a+2)(b+1)=32(a>0,b>0)且ab=30–(a+2b)
应用重要不等式a+2b=(a+2)+(2b+2)–4≥
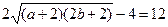
∴ab≤18,当且仅当a=2b时等号成立
将a=2b代入①得a=6,b=3.
故当且仅当a=6,b=3时,经沉淀后流出的水中该杂质的质量分数最小.
解法二:由2a+4b+2ab=60,得
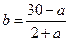 ,
,记
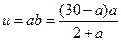 (0<a<30)则要求y的最小值只须求u的最大值.
(0<a<30)则要求y的最小值只须求u的最大值.由
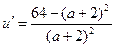 ,令u′=0得a=6
,令u′=0得a=6且当0<a<6时,u′>0,当6<u<30时u′<0,
∴
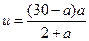 在a=6时取最大值,此时b=3.
在a=6时取最大值,此时b=3.从而当且仅当a=6,b=3时,y=
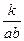 取最小值.
取最小值. 
练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 +
+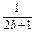 +
+ 的最小值.
的最小值.
 ,则下列不等式:①
,则下列不等式:①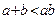 ;②
;② ;③
;③ ;④
;④ 中,正确的不等式有( )
中,正确的不等式有( ) 的最小值
的最小值
 满足
满足 ,求
,求 的最小值。
的最小值。 ,则的整数部分是( )
,则的整数部分是( ) ,则函数
,则函数 的最小值为 .
的最小值为 .