题目内容
已知△ABC的三边长分别为a、b、c,且满足abc=
(1)是否存在边长均为整数的△ABC?若存在,求出三边长;若不存在,说明理由。
(2)若a>1,b>1,c>1,求出△ABC周长的最小值。

(1)是否存在边长均为整数的△ABC?若存在,求出三边长;若不存在,说明理由。
(2)若a>1,b>1,c>1,求出△ABC周长的最小值。
(1)存在三边长均为整数的△ABC,其三边长分别为4,5,6或3,7,8,(2)△ABC的周长最小值为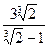 ,当且仅当
,当且仅当 时,取得此最小值
时,取得此最小值
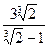 ,当且仅当
,当且仅当 时,取得此最小值
时,取得此最小值(1)不妨设整数a≥b≥c,显然c≥2。
若c≥5,这时
由 ,可得
,可得
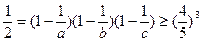 。
。
矛盾。
故c只可能取2,3,4。
当c=2时, ,有
,有
又a≥b≥2,故无解。
当c=3时, ,即
,即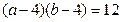
又a≥b≥3,故
 或
或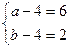 或
或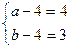
解得 或
或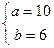 或
或
能构成三角形的只有a=8,b=7,c=3。
当c=4时,同理解得a=9,b=4或a=6,b=5。
能构成三角形的只有a=6,b=5,c=4。
故存在三边长均为整数的△ABC,其三边长分别为4,5,6或3,7,8
(2)由 ,可得
,可得
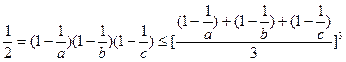
所以,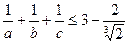
又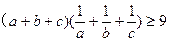 ,则有
,则有

故△ABC的周长最小值为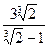 ,当且仅当
,当且仅当 时,取得此最小值。
时,取得此最小值。
若c≥5,这时

由
 ,可得
,可得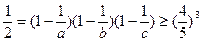 。
。矛盾。
故c只可能取2,3,4。
当c=2时,
 ,有
,有
又a≥b≥2,故无解。
当c=3时,
 ,即
,即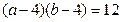
又a≥b≥3,故
 或
或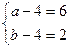 或
或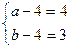
解得
 或
或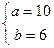 或
或
能构成三角形的只有a=8,b=7,c=3。
当c=4时,同理解得a=9,b=4或a=6,b=5。
能构成三角形的只有a=6,b=5,c=4。
故存在三边长均为整数的△ABC,其三边长分别为4,5,6或3,7,8
(2)由
 ,可得
,可得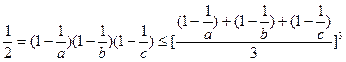
所以,
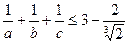
又
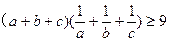 ,则有
,则有
故△ABC的周长最小值为
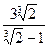 ,当且仅当
,当且仅当 时,取得此最小值。
时,取得此最小值。
练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
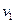 行驶,在后一半时间以速度
行驶,在后一半时间以速度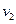 行驶,乙在前一半路程以速度
行驶,乙在前一半路程以速度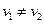 ).则下列说法正确的是
).则下列说法正确的是 ,x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.
,x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.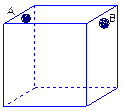
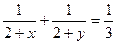 ,则xy的最小值为
,则xy的最小值为 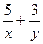 =2(x>0,y>0),则xy的最小值是 。
=2(x>0,y>0),则xy的最小值是 。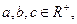 求
求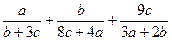 的最小值
的最小值 的最小值是 。
的最小值是 。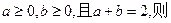 ( )
( )


