题目内容
设a,b,c∈R+且a+b+c=1,试求: +
+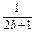 +
+ 的最小值.
的最小值.
 +
+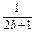 +
+ 的最小值.
的最小值. +
+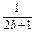 +
+ 取最小值
取最小值
解 ∵a+b+c=1,a、b、c为正数,
∴ (2a+1+2b+1+2c+1)
(2a+1+2b+1+2c+1)
≥(1+1+1)2,
∴ +
+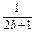 +
+ ≥
≥ .
.
当且仅当2a+1=2b+1=2c+1,即a=b=c时“=”成立,
∴当a=b=c=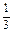 时,
时, +
+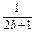 +
+ 取最小值
取最小值 .
.
∴
 (2a+1+2b+1+2c+1)
(2a+1+2b+1+2c+1)≥(1+1+1)2,
∴
 +
+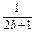 +
+ ≥
≥ .
.当且仅当2a+1=2b+1=2c+1,即a=b=c时“=”成立,
∴当a=b=c=
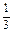 时,
时, +
+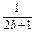 +
+ 取最小值
取最小值 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
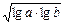 ,Q=
,Q=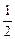 (lga+lgb),R=lg(
(lga+lgb),R=lg(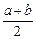 ),则
),则 ,x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.
,x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l. m和汽车车速
m和汽车车速 km/h有如下关系:
km/h有如下关系: .
.
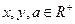 ,且
,且 恒成立,则
恒成立,则 的最小值是( )
的最小值是( )

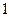

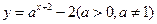 的图象恒过定点A,若点A在直线
的图象恒过定点A,若点A在直线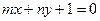 上,其中
上,其中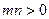 ,则
,则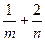 的最小值为 .
的最小值为 . 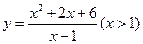 的最小值为( )
的最小值为( )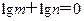 ,那么
,那么 的最小值是 .
的最小值是 .