题目内容
某校一年级为配合素质教育,利用一间教室作为学生绘画成果展览室,为节约经费,他们利用课桌作为展台,将装画的镜框放置桌上,斜靠展出,已知镜框对桌面的倾斜角为α(90°≤α<180°)镜框中,画的上、下边缘与镜框下边缘分别相距a m,b m,(a>b). 问学生距离镜框下缘多远看画的效果最佳?
学生距离镜框下缘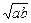 cm处时,视角最大,即看画效果最佳
cm处时,视角最大,即看画效果最佳
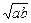 cm处时,视角最大,即看画效果最佳
cm处时,视角最大,即看画效果最佳 建立如图所示的直角坐标系,AO为镜框边,AB为画的宽度,O为下边缘上的一点,在x轴的正半轴上找一点C(x,0)(x>0),欲使看画的效果最佳,应使∠ACB取得最大值.
由三角函数的定义知:A、B两点坐标分别为(acosα,asinα)、
(bcosα,bsinα),于是直线AC、BC的斜率分别为:
kAC=tanxCA=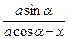 ,
,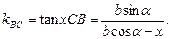
于是
tanACB=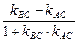
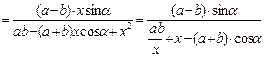
由于∠ACB为锐角,且x>0,则tanACB≤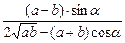 ,
,
当且仅当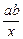 =x,即x=
=x,即x=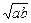 时,等号成立,
时,等号成立,
此时∠ACB取最大值,对应的点为C(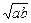 ,0),
,0),
因此,学生距离镜框下缘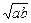 cm处时,视角最大,即看画效果最佳.
cm处时,视角最大,即看画效果最佳.
由三角函数的定义知:A、B两点坐标分别为(acosα,asinα)、
(bcosα,bsinα),于是直线AC、BC的斜率分别为:
kAC=tanxCA=
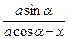 ,
,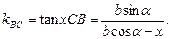
于是
tanACB=
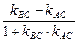
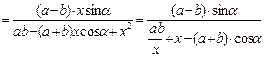
由于∠ACB为锐角,且x>0,则tanACB≤
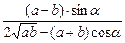 ,
,当且仅当
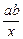 =x,即x=
=x,即x=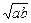 时,等号成立,
时,等号成立,此时∠ACB取最大值,对应的点为C(
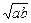 ,0),
,0),因此,学生距离镜框下缘
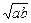 cm处时,视角最大,即看画效果最佳.
cm处时,视角最大,即看画效果最佳. 
练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
 m和汽车车速
m和汽车车速 km/h有如下关系:
km/h有如下关系: .
.
 .根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.
.根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.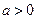 且
且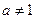 时,函数
时,函数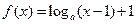 的图像恒过点
的图像恒过点 ,若点
,若点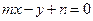 上,则
上,则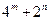 的最小值为
的最小值为 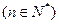 .
. ,且
,且 ,则
,则 的最大值为
的最大值为
 ,则
,则 的最大值为 ▲ .
的最大值为 ▲ .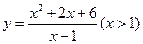 的最小值为( )
的最小值为( )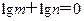 ,那么
,那么 的最小值是 .
的最小值是 .