题目内容
14.已知y=f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x-x2.(Ⅰ)求y=f(x)的解析式;
(Ⅱ)问是否存在这样的正数a,b使得当x∈[a,b]时,函数g(x)=f(x)的值域为[$\frac{1}{b}$,$\frac{1}{a}$],若存在,求出所有a,b的值,若不存在,说明理由.
分析 (1)令x<0,则-x>0,由当x>0时,f(x)=2x-x2,可得f(-x)的表达式,进而根据f(x)为奇函数,f(x)=-f(-x),可得答案;
(Ⅱ)分0<a<b≤1,0<a<1<b和1≤a<b三种情况分别讨论,a,b的取值情况,最后综合讨论结果可得答案.
解答 解:(Ⅰ)设x<0,则-x>0,
由f(x)=-f(-x)=-[2(-x)-(-x)2]=2x+x2,
当x=0时,f(x)=0,
故f(x)=$\left\{\begin{array}{l}{x}^{2}+2x,x≤0\\{-x}^{2}+2x,x>0\end{array}\right.$;
(2)分下述三种情况:
①0<a<b≤1,那么$\frac{1}{a}$>1,而当x≥0,f(x)的最大值为1,
故此时不可能使g(x)=f(x),
②若0<a<1<b,此时若g(x)=f(x),
则g(x)的最大值为g(1)=f(1)=1,得a=1,这与0<a<1<b矛盾;
③若1≤a<b,因为x≥1时,f(x)是减函数,则f(x)=2x-x2,
于是有$\left\{\begin{array}{l}\frac{1}{b}=g(b)=-{b}^{2}+2b\\ \frac{1}{a}=g(a)=-{a}^{2}+2a\end{array}\right.$?$\left\{\begin{array}{l}(a-1)({a}^{2}-a+1)=0\\(b-1)({b}^{2}-b+1)=0\end{array}\right.$,
考虑到1≤a<b,
解得a=1,b=$\frac{1+\sqrt{5}}{2}$
点评 本题考查的知识点是函数奇偶性的性质,函数解析式的求解及常方法,二次函数的性质,其中利用奇函数的性质,求出函数的解析式,并分析其性质是解答本题的关键.

| A. | -1 | B. | 1 | C. | $\sqrt{5}$ | D. | $-\sqrt{5}$ |
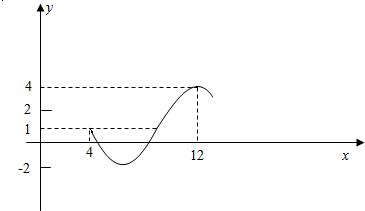 如图为函数y=Asin(ωx+ϕ)+c(A>0,ω>0,ϕ>0)图象的一部分,求此函数的解析式.
如图为函数y=Asin(ωx+ϕ)+c(A>0,ω>0,ϕ>0)图象的一部分,求此函数的解析式.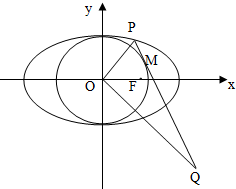 在平面直角坐标系xoy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F(1,0),点P在椭圆C上,且在第一象限内,直线PQ与圆O:x2+y2=b2相切于点M.
在平面直角坐标系xoy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F(1,0),点P在椭圆C上,且在第一象限内,直线PQ与圆O:x2+y2=b2相切于点M.