题目内容
9.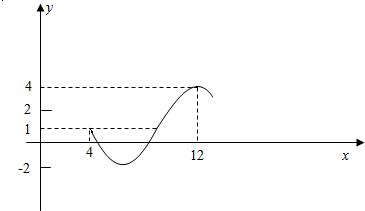 如图为函数y=Asin(ωx+ϕ)+c(A>0,ω>0,ϕ>0)图象的一部分,求此函数的解析式.
如图为函数y=Asin(ωx+ϕ)+c(A>0,ω>0,ϕ>0)图象的一部分,求此函数的解析式.
分析 根据三角函数的图象求出A,ω,ϕ,即可确定函数的解析式;
解答 解:由函数的图象可知函数的最大值为A+c=4,最小值为-A+c=-2,
∴c=1,A=3,
∵$\frac{3}{4}$T=12-4=8,
∴函数的周期T=$\frac{32}{3}$.
即 $\frac{2π}{ω}$=$\frac{32}{3}$,解得:?=$\frac{3π}{16}$,
∴y=3sin($\frac{3π}{16}$x+ϕ)+1
∵(12,4)在函数图象上
∴4=3sin($\frac{3π}{16}$•12+ϕ)+1,
即sin($\frac{9π}{4}$+ϕ)=1
∴$\frac{9π}{4}$+ϕ=$\frac{π}{2}$+2kπ,k∈Z,
得ϕ=-$\frac{7π}{4}$+2kπ,k∈Z
∴函数解析式为y=3sin($\frac{3π}{16}$•x+$\frac{π}{4}$)+1.
点评 本题主要考查三角函数解析式的求法,根据三角函数的图象是解决本题的关键,要求熟练掌握三角函数的图象和性质.

练习册系列答案
相关题目
17.函数y=lg$\frac{x-3}{x+3}$的图象( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于直线y=x对称 | D. | 关于原点对称 |
1. 某校高三期末统一测试,随机抽取一部分学生的数学成绩分组统计如下表:
某校高三期末统一测试,随机抽取一部分学生的数学成绩分组统计如下表:
(Ⅰ)若全校参加本次考试的学生有600人,试估计这次测试中我区成绩在90分以上的人数;
(Ⅱ)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分的概率.
 某校高三期末统一测试,随机抽取一部分学生的数学成绩分组统计如下表:
某校高三期末统一测试,随机抽取一部分学生的数学成绩分组统计如下表:| 分组 | 频数 | 频率 |
| (0,30] | 3 | 0.03 |
| (30,60] | 3 | 0.03 |
| (60,90] | 37 | 0.37 |
| (90,120] | m | n |
| (120,150] | 15 | 0.15 |
| 合计 | M | N |
(Ⅱ)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分的概率.