题目内容
如图,已知高为3的棱柱ABC-A1B1C1的底面是边长为1的正三角形,求三棱锥B1-ABC的体积。
解:三棱锥B1-ABC的高h=3,底面积S=S△ABC= ×12=
×12= ,
,
则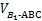 =
= Sh=
Sh= ×
× ×3=
×3= .
.
解析

练习册系列答案
相关题目
题目内容
如图,已知高为3的棱柱ABC-A1B1C1的底面是边长为1的正三角形,求三棱锥B1-ABC的体积。
解:三棱锥B1-ABC的高h=3,底面积S=S△ABC= ×12=
×12= ,
,
则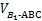 =
= Sh=
Sh= ×
× ×3=
×3= .
.
解析
