题目内容
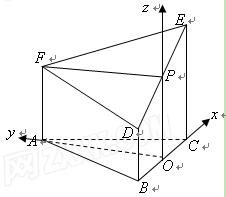
(本小题满分12分)如图所示的几何体是由以等边三角形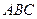 为底面的棱柱被平面
为底面的棱柱被平面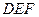 所截而得,已
所截而得,已 知
知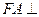 平面
平面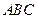 ,
, ,
, ,
,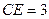 ,
,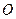 为
为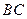 的中点,
的中点,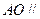 面
面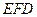 .
.
(Ⅰ)求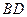 的长;
的长;
(Ⅱ)求证:面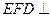 面
面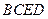 ;
;
(Ⅲ)求平面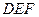 与平面
与平面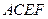 相交所成锐角二面角的余弦值.
相交所成锐角二面角的余弦值.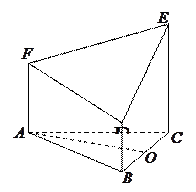
(Ⅰ)取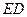
 的中点
的中点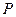 ,连接
,连接
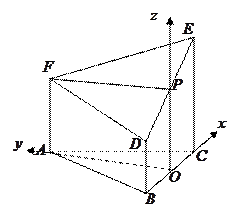
则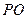 为梯形
为梯形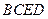 的中位线,
的中位线,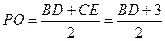
又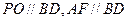 ,所以
,所以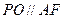
所以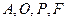 四点共面……………2分
四点共面……………2分
因为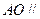 面
面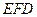 ,且面
,且面 面
面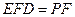
所以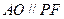
所以四边形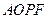 为平行四边形,
为平行四边形,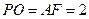
所以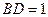 ……………4分
……………4分
(Ⅱ)由题意可知平面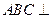 面
面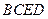 ;
;
又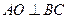 且
且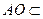 平面
平面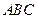
所以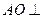 面
面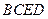
因为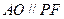 所以
所以 面
面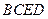
又 面
面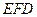 ,所以面
,所以面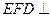 面
面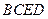 ;……………6分
;……………6分
(Ⅲ)以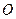 为原点,
为原点,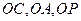 所在直线分别为
所在直线分别为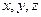 轴建立空间直角坐标系
轴建立空间直角坐标系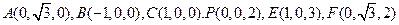 ……7分
……7分
设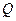 为
为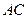 的中点,则
的中点,则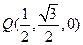
易证: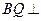 平面
平面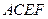
平面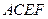 的法向量为
的法向量为 ……………8分
……………8分
设平面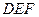 的法向量为
的法向量为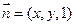 ,
,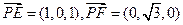
由 得
得 所以
所以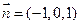 ……………10分
……………10分
所以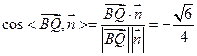 ,……………11分
,……………11分
所以平面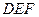 与平面
与平面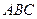 相交所成锐角二面角的余弦值为
相交所成锐角二面角的余弦值为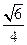 . ……12分
. ……12分
解析

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
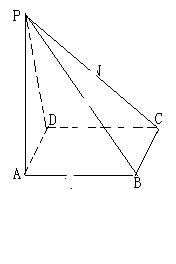
 的底面是边长为1的正方形,
的底面是边长为1的正方形,
 平面
平面
 中,
中,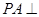 底面
底面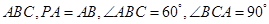 , 点
, 点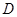 ,
, 分别在棱
分别在棱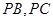 上,且
上,且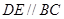
 平面
平面 ;
;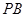 的中点时,求
的中点时,求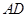 与平面
与平面


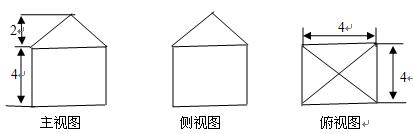

 (2)求该几何题的表面积。
(2)求该几何题的表面积。 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点,作
,E是PC的中点,作 交PB于点F.
交PB于点F. 的体积.
的体积.