题目内容
5.已知函数f(x)=sin(ωx+φ)+k(A>0,|φ|<$\frac{π}{2}$)的最大值为3,最小值为1,最小正周期为π,直线x=$\frac{π}{3}$是其图象的一条对称轴,将函数f(x)的图象向左平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)的解析式可以为( )| A. | g(x)=sin2x+2 | B. | g(x)=sin(2x+$\frac{π}{6}$)+2 | C. | g(x)=sin(2x+$\frac{π}{6}$)+1 | D. | g(x)=sin(4x-$\frac{π}{3}$)+2 |
分析 由题意求出A,T,解出ω,直线x=$\frac{π}{3}$是其图象的一条对称轴,求出φ,得到函数解析式,由函数y=Asin(ωx+φ)的图象变换即可得解.
解答 解:由题意可知ω=$\frac{2π}{π}$=2,2×$\frac{π}{3}$+φ=kπ+$\frac{π}{2}$,φ=kπ-$\frac{π}{6}$,取k=0,可得φ=-$\frac{π}{6}$,
故可得:f(x)=sin(2x-$\frac{π}{6}$)+2,
将函数f(x)的图象向左平移$\frac{π}{6}$个单位得到函数g(x)的解析式为:g(x)=sin[2(x+$\frac{π}{6}$)-$\frac{π}{6}$]+2=sin(2x+$\frac{π}{6}$)+2,
故选:B.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换,考查学生分析问题解决问题的能力,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
6.在平面直角坐标系中,O为坐标原点,A(1,0),B(0,-$\sqrt{3}$),点D是圆C:(x+1)2+y2=1上的动点,则|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$|的最大值为( )
| A. | 2 | B. | $\sqrt{3}$+1 | C. | $\sqrt{3}$+$\sqrt{2}$ | D. | $\sqrt{3}$+2 |
7.“a=1”是“直线l:y=kx+a与圆C:x2-2x+y2=0相交”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
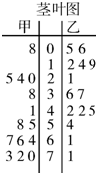 为了调查甲、乙两个交通站的车流量,随机选取了14天,统计每天上午8:00-12:00间各自的车流量(单位:百辆),得如下所示的统计图,
为了调查甲、乙两个交通站的车流量,随机选取了14天,统计每天上午8:00-12:00间各自的车流量(单位:百辆),得如下所示的统计图,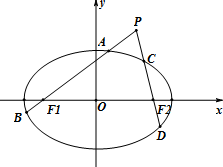 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,它的四个顶点连成的菱形的面积为8$\sqrt{2}$.过动点P(不在x轴上)的直线PF1,PF2与椭圆的交点分别为A,B和C,D.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,它的四个顶点连成的菱形的面积为8$\sqrt{2}$.过动点P(不在x轴上)的直线PF1,PF2与椭圆的交点分别为A,B和C,D.