题目内容
已知双曲线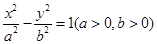 ,若过右焦点F且倾斜角为30°的直线与双曲线的右支有两个交点,则此双曲线离心率的取值范围是__________.
,若过右焦点F且倾斜角为30°的直线与双曲线的右支有两个交点,则此双曲线离心率的取值范围是__________.
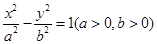 ,若过右焦点F且倾斜角为30°的直线与双曲线的右支有两个交点,则此双曲线离心率的取值范围是__________.
,若过右焦点F且倾斜角为30°的直线与双曲线的右支有两个交点,则此双曲线离心率的取值范围是__________.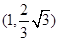
试题分析:易知:直线的斜率为
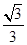 ,要满足直线方程与双曲线右支有两个交点,需
,要满足直线方程与双曲线右支有两个交点,需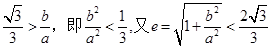 ,所以双曲线离心率的取值范围是
,所以双曲线离心率的取值范围是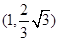 。
。点评:要使此直线与双曲线的右支有两个交点,需满足此直线的斜率比过一三象限的渐近线的斜率大,分析出这一条是解题的关键。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
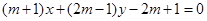 经过的定点的坐标是 .
经过的定点的坐标是 .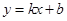 与曲线
与曲线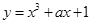 相切于点
相切于点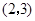 ,则
,则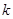 的值为 ( )
的值为 ( )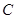 的中心在原点,焦点在
的中心在原点,焦点在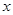 轴上,一条经过点
轴上,一条经过点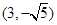 且方向向量为
且方向向量为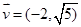 的直线
的直线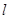 交椭圆
交椭圆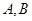 两点,交
两点,交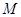 点,且
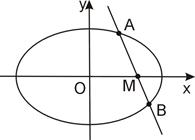
点,且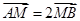 .
.
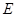 :
: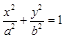 (
(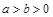 )过点
)过点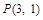 ,其左、右焦点分别为
,其左、右焦点分别为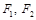 ,且
,且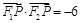 .
.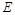 的方程;
的方程;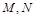 是直线
是直线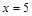 上的两个动点,且
上的两个动点,且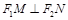 ,则以
,则以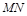 为直径的圆
为直径的圆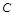 是否过定点?请说明理由.
是否过定点?请说明理由.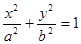 (
(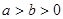 )过点
)过点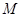 (0,2),离心率
(0,2),离心率 .
.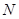 (2,0)的直线
(2,0)的直线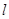 与椭圆相交于
与椭圆相交于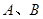 两点,且
两点,且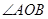 为锐角(其中
为锐角(其中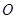 为坐标原点),求直线
为坐标原点),求直线 0)的焦点F的直线交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3.则此抛物线的方程为( )
0)的焦点F的直线交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3.则此抛物线的方程为( )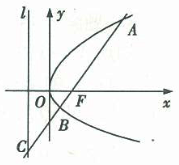
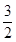 x
x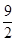 x
x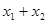 =6,那么
=6,那么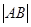 =
=