题目内容

一个平整的操场上竖立着两根相距20米的旗杆，旗杆高度分别为5米和8米，地面上动点P满足：从P处分别看两旗杆顶部，两个仰角总相等，则P的轨迹是（　　）
A．直线B．线段C．圆D．椭圆
设两根旗杆AC、BD分别在地面A、B两处，不妨设AC=5m，BD=8m，地面上的动点P到两旗杆顶点的仰角相等，设满足条件的点为P，则直角三角形PAC与直角三角形PBD相似，因此PA：PB=5：8．
在地面上以AB所在直线为x轴，以AB的中点0为坐标原点，建立平面直角坐标系，设P（x，y），A（0，10），
B（0，-10），则
x2+(y-10)2
：
x2+(y+10)2
=5：8，
化简整理得：39x2+39y2-1760y+3900=0，因此点P的轨迹是圆．
故选C．
练习册系列答案
相关题目
已知A（1，0），B（4，0），动点T（x，y）满足
|TA|
|TB|
=
1
2
，设动点T的轨迹是曲线C，直线l：y=kx+1与曲线C交于P，Q两点．
（1）求曲线C的方程；
（2）若
OP
•
OQ
=-2，求实数k的值；
（3）过点（0，1）作直线l1与l垂直，且直线l1与曲线C交于M，N两点，求四边形PMQN面积的最大值．
已知长为
2
+1的线段AB的两个端点A、B分别在x轴、y轴上滑动，P是AB上的一点，且
AP
=
2
2
PB
，则点P的轨迹方程为______．
设定点M（-3，4），动点N在圆x2+y2=4上运动，以OM、ON为邻边作平行四边形MONP，则点P的轨迹方程为______．
已知与曲线C：x2+y2-2x-2y+1=0相切的直线l交x轴、y轴于A、B两点，O为原点，且|OA|=a，|OB|=b，（a＞2，b＞2）．
（1）求证：曲线C与直线l相切的条件是（a-2）（b-2）=2；
（2）求线段AB中点的轨迹方程．
△ABC的两个顶点坐标分别是B（0，-2）和C（0，2），顶点A满足sinB+sinC=
3
2
sinA．
（1）求顶点A的轨迹方程；
（2）若点P（x，y）在（1）轨迹上，求μ=2x-y的最值．
已知F1（-5，0），F2（5，0），动点P（x，y）满足|PF1|-|PF2|=10，则动点P的轨迹方程是______．
已知动圆过定点P（1，0），且与定直线l：x=-1相切；
（1）求动圆圆心M的轨迹方程；
（2）设过点P且斜率为-
3
的直线与曲线M相交于A、B两点，求线段AB的长．
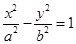
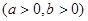已知双曲线的渐近线方程为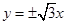，则以它的顶点为焦点，焦点为顶点的椭圆的离心率等于（  ）
A．B．C．D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网