题目内容
△ABC的两个顶点坐标分别是B(0,-2)和C(0,2),顶点A满足sinB+sinC=
sinA.
(1)求顶点A的轨迹方程;
(2)若点P(x,y)在(1)轨迹上,求μ=2x-y的最值.
| 3 |
| 2 |
(1)求顶点A的轨迹方程;
(2)若点P(x,y)在(1)轨迹上,求μ=2x-y的最值.
(1)由正弦定理知2R|AC|+2R|AB|=
|BC|•2R
∴|AC|+|AB|=
|BC|=6>|BC|=4
∴A的轨迹是以B、C为焦点的椭圆,其中长短轴长a=3,半焦距为c=2
∴A的轨迹方程为
+
=1(x≠0)…(6分)
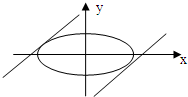
(2)如图,当直线μ=2x-y平移到l1与椭圆相切时,取最小,当直线μ=2x-y平移到l2与椭圆相切时,取最大,
当x=0时,y=±3,此时μ=±3不为最值
∴μmax=
,μmin=-
| 3 |
| 2 |
∴|AC|+|AB|=
| 3 |
| 2 |
∴A的轨迹是以B、C为焦点的椭圆,其中长短轴长a=3,半焦距为c=2
∴A的轨迹方程为
| y2 |
| 9 |
| x2 |
| 5 |
(2)如图,当直线μ=2x-y平移到l1与椭圆相切时,取最小,当直线μ=2x-y平移到l2与椭圆相切时,取最大,
|
当x=0时,y=±3,此时μ=±3不为最值
∴μmax=
| 29 |
| 29 |


练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目

 ,0)和F2(
,0)和F2( ·
·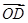 =0(O为坐标原点),求直线l的方程.
=0(O为坐标原点),求直线l的方程.