题目内容
(本小题满分13分)
已知函数 .
.
(1)若 ,且
,且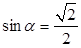 ,求
,求 的值;
的值;
(2)求函数 的最小正周期及单调递增区间.
的最小正周期及单调递增区间.
(1)  ;(2)
;(2) 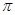 ,
,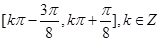
解析试题分析:(1)由 ,且
,且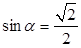 ,求出角
,求出角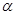 的余弦值,再根据函数
的余弦值,再根据函数 ,即可求得结论.
,即可求得结论.
(2) 已知函数 ,由正弦与余弦的二倍角公式,以及三角函数的化一公式,将函数
,由正弦与余弦的二倍角公式,以及三角函数的化一公式,将函数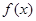 化简.根据三角函数周期的公式即可的结论.根据函数的单调递增区间,通过解不等式即可得到所求的结论.
化简.根据三角函数周期的公式即可的结论.根据函数的单调递增区间,通过解不等式即可得到所求的结论.
试题解析: (1)因为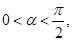
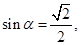 所以
所以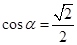 .所以
.所以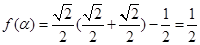
(2)因为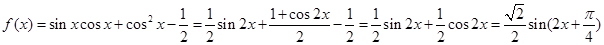 ,所以
,所以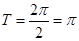 .由
.由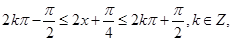 得
得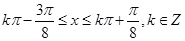 .所以
.所以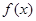 的单调递增区间为
的单调递增区间为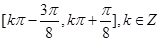 .
.
考点:1.三角函数的性质.2.三角的恒等变形.

练习册系列答案
相关题目
某同学用“五点法”画函数 在某一个周期内的图象时,列表并填入的部分数据如下表:
在某一个周期内的图象时,列表并填入的部分数据如下表:
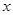 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
(1)请求出上表中的
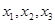 ,并直接写出函数
,并直接写出函数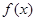 的解析式;
的解析式;(2)将
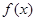 的图象沿
的图象沿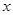 轴向右平移
轴向右平移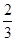 个单位得到函数
个单位得到函数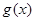 ,若函数
,若函数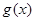 在
在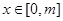 (其中
(其中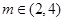 )上的值域为
)上的值域为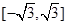 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为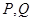 ,求
,求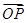 与
与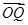 夹角
夹角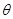 的大小。
的大小。 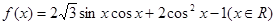
 的最小正周期及在区间
的最小正周期及在区间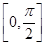 上的最大值和最小值;
上的最大值和最小值;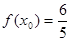 ,
,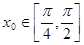 ,求
,求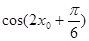 的值.
的值.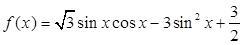 .
. 的最小正周期;
的最小正周期;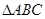 中,角
中,角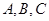 所对的边长分别为
所对的边长分别为 ,若
,若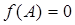 ,
,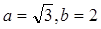 ,求
,求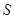 .
. 为奇函数,且
为奇函数,且 ,其中
,其中 .
. 的值;
的值; ,求
,求 的值.
的值. .
. 的值;
的值; 的值.
的值. ,若直线
,若直线 是函数
是函数 图象的一条切线.
图象的一条切线. 、
、 的横坐标依次为2和4,
的横坐标依次为2和4, 为坐标原点,求△
为坐标原点,求△ 的面积.
的面积.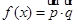 ,而
,而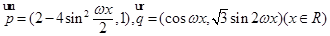 .
.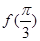 最大,求
最大,求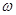 能取到的最小正数值.
能取到的最小正数值.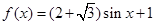 且
且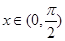 ,求
,求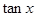 .
.